Dots + interval stats and geoms

Introduction

This vignette describes the dots+interval geoms and stats in ggdist. This is a flexible sub-family of stats and geoms designed to make plotting dotplots straightforward. In particular, it supports a selection of useful layouts (including the classic Wilkinson layout, a weave layout, and a beeswarm layout) and can automatically select the dot size so that the dotplot stays within the bounds of the plot.

Setup

The following libraries are required to run this vignette:

library(dplyr)
library(tidyr)
library(distributional)
library(ggdist)
library(ggplot2)
library(patchwork)

theme_set(theme_ggdist())

Anatomy of `geom_dotsinterval()`

The dotsinterval family of geoms and stats is a sub-family of slabinterval (see vignette("slabinterval")), where the “slab” is a collection of dots forming a dotplot and the interval is a summary point (e.g., mean, median, mode) with an arbitrary number of intervals.

The base geom_dotsinterval() uses a variety of custom aesthetics to create the composite geometry:

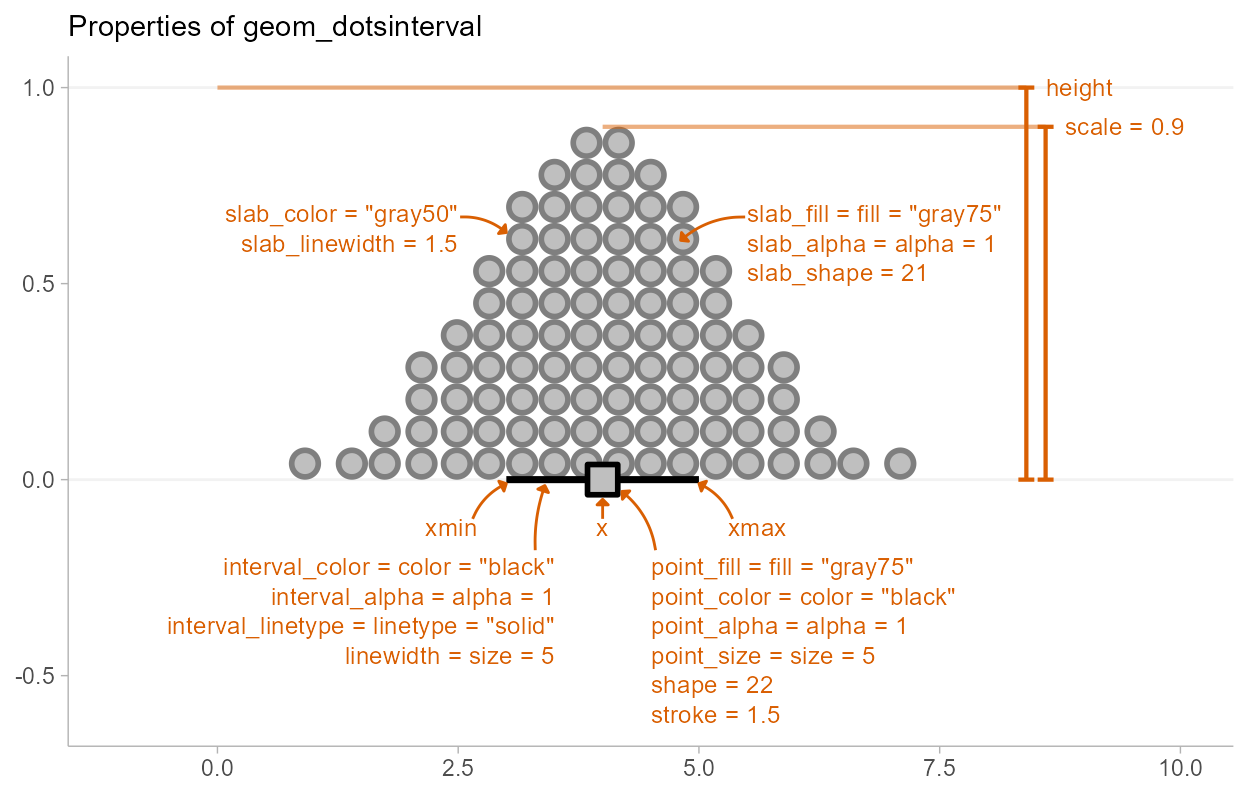
Depending on whether you want a horizontal or vertical orientation, you can provide ymin and ymax instead of xmin and xmax. By default, some aesthetics (e.g., fill, color, size, alpha) set properties of multiple sub-geometries at once. For example, the color aesthetic by default sets both the color of the point and the interval, but can also be overridden by point_color or interval_color to set the color of each sub-geometry separately.

Due to its relationship to the geom_slabinterval() family, aesthetics specific to the “dots” sub-geometry are referred to with the prefix slab_. When using the standalone geom_dots() geometry, it is not necessary to use these custom aesthetics:

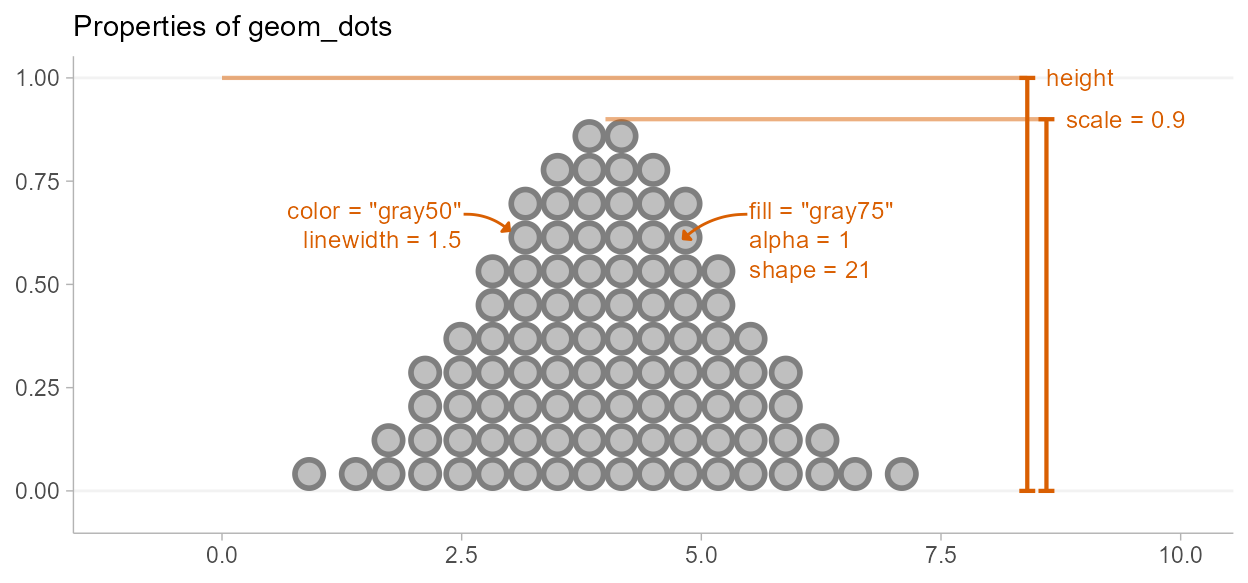
geom_dotsinterval() is often most useful when paired with stat_dotsinterval(), which will automatically calculate points and intervals and map these onto endpoints of the interval sub-geometry.

stat_dotsinterval() and stat_dots() can be used on two types of data, depending on what aesthetic mappings you provide:

Sample data; e.g. draws from a data distribution, bootstrap distribution, Bayesian posterior distribution (or any other distribution, really). To use the stats on sample data, map sample values onto the x or y aesthetic.
Distribution objects and analytical distributions. To use the stats on this type of data, you must use the xdist, or ydist aesthetics, which take distributional objects, posterior::rvar() objects, or distribution names (e.g. "norm", which refers to the Normal distribution provided by the dnorm/pnorm/qnorm functions). When used on analytical distributions (e.g. distributional::dist_normal()), the quantiles argument determines the number of quantiles used (and therefore the number of dots shown); the default is 100.

All dotsinterval geoms can be plotted horizontally or vertically. Depending on how aesthetics are mapped, they will attempt to automatically determine the orientation; if this does not produce the correct result, the orientation can be overridden by setting orientation = "horizontal" or orientation = "vertical".

Controlling dot layout

Size and layout of dots in the dotplot are controlled by four parameters: scale, binwidth, dotsize, and stackratio.

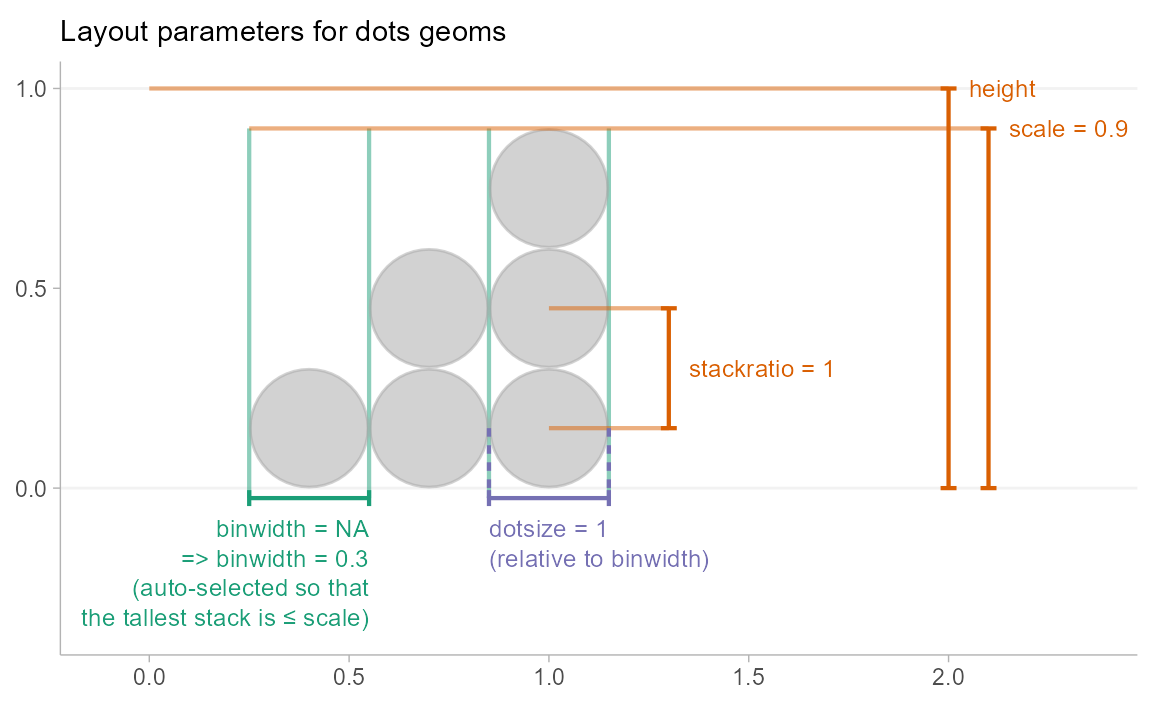
scale: If binwidth is not set (is NA), then the binwidth is determined automatically so that the height of the highest stack of dots is less than scale. The default value of scale, 0.9, ensures there is a small gap between dotplots when multiple dotplots are drawn.
binwidth: The width of the bins used to lay out the dots:
- NA (default): Use scale to determine bin width.
- A single numeric or unit(): the exact bin width to use. If it is numeric, the bin width is expressed in data units; use unit() to specify the width in terms of screen coordinates (e.g. unit(0.1, "npc") would make the bin width 0.1 normalized parent coordinates, which would be 10% of the plot width.)
- A 2-vector of numerics or unit()s giving an acceptable minimum and maximum width. The automatic bin width algorithm will attempt to find the largest bin width between these two values that also keeps the tallest stack of dots shorter than scale.
dotsize: The size of the dots as a percentage of binwidth. The default value is 1.07 rather than 1. This value was chosen largely by trial and error, to find a value that gives nice-looking layouts with circular dots on continuous distributions, accounting for the fact that a slight overlap of dots tends to give a nicer apparent visual distance between adjacent stacks than the precise value of 1.
stackratio: The distance between the centers of dots in a stack as a proportion of the height of each dot. stackratio = 1, the default, mean dots will just touch; stackratio < 1 means dots will overlap each other, and stackratio > 1 means dots will have gaps between them.

Side

The side aesthetic allows you to adjust the positioning and direction of the dots:

"top", "right", or "topright": draw the dots on the top or on the right, depending on orientation
"bottom", "left", or "bottomleft": draw the dots on the bottom or on the left, depending on orientation
"topleft": draw the dots on top or on the left, depending on orientation
"bottomright": draw the dots on the bottom or on the right, depending on orientation
"both": draw the dots mirrored, as in a “beeswarm” plot.

When orientation = "horizontal", this yields:

set.seed(1234)
x = rnorm(100)

side_plot = function(...) {
  expand.grid(
    x = x,
    side = c("topright", "both", "bottomleft"),
    stringsAsFactors = FALSE
  ) %>%
    ggplot(aes(side = side, ...)) +
    geom_dots() +
    facet_grid(~ side, labeller = "label_both") +
    labs(x = NULL, y = NULL) +
    theme(panel.border = element_rect(color = "gray75", fill = NA))
}
side_plot(x = x) +
  labs(title = "Horizontal geom_dots() with different values of side") +
  scale_y_continuous(breaks = NULL)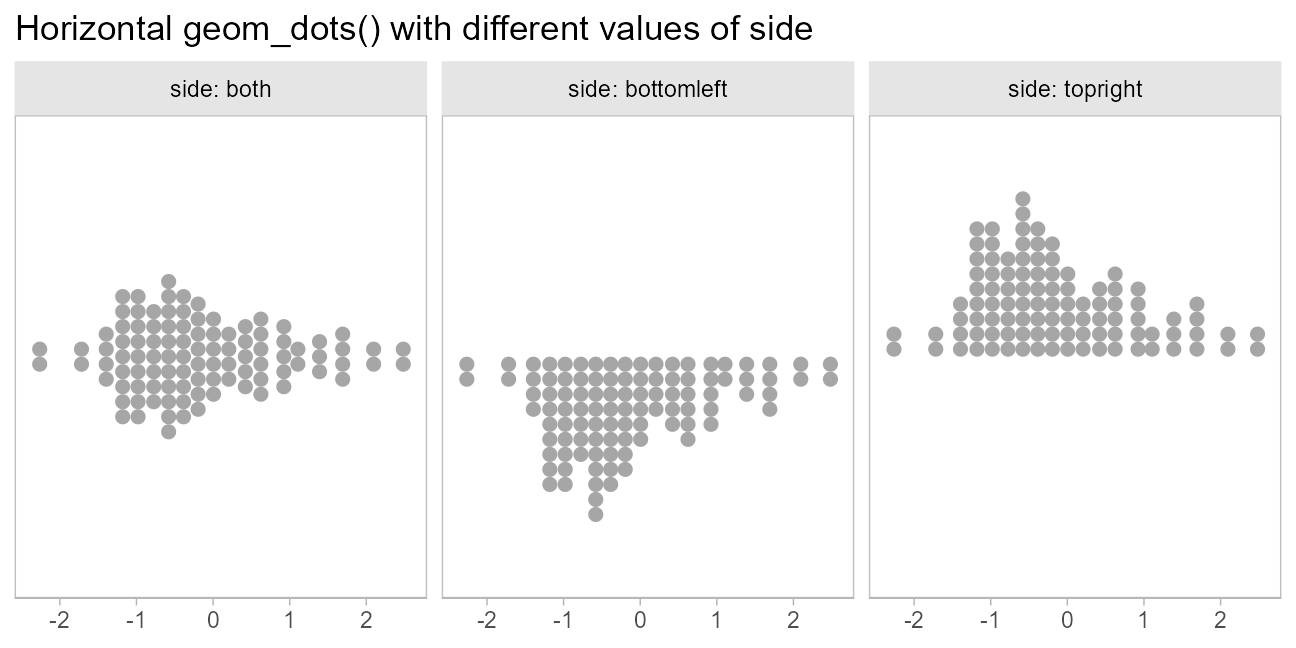

When orientation = "vertical", this yields:

side_plot(y = x) +
  labs(title = "Vertical geom_dots() with different values of side") +
  scale_x_continuous(breaks = NULL)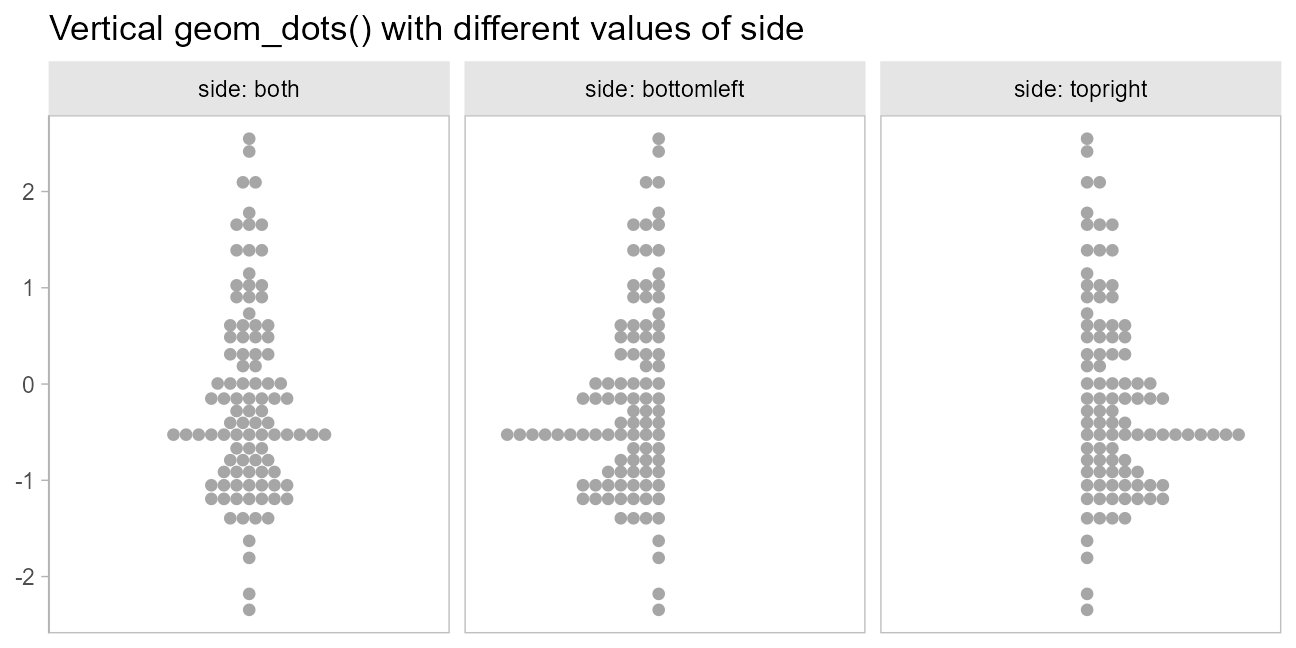

Layout

The layout parameter allows you to adjust the algorithm used to place dots:

"bin" (default): places dots on the off-axis at the midpoint of their bins as in the classic Wilkinson dotplot. This maintains the alignment of rows and columns in the dotplot. This layout is slightly different from the classic Wilkinson algorithm in that: (1) it nudges bins slightly to avoid overlapping bins and (2) if the input data are symmetrical it will return a symmetrical layout.
"weave": uses the same basic binning approach of “bin”, but places dots in the off-axis at their actual positions (modulo overlaps, which are nudged out of the way). This maintains the alignment of rows but does not align dots within columns.
"hex": uses the same basic binning approach of “bin”, but alternates placing dots +binwidth/4 or -binwidth/4 in the off-axis from the bin center. This allows hexagonal packing by setting a stackratio less than 1 (something like 0.9 tends to work).
“swarm”: uses the "compactswarm" layout from beeswarm::beeswarm(). Does not maintain alignment of rows or columns, but can be more compact and neat looking, especially for sample data (as opposed to quantile dotplots of theoretical distributions, which may look better with "bin", "weave", or "hex").

When side is "top", these layouts look like this:

layout_plot = function(layout, side, ...) {
  data.frame(
    x = x
  ) %>%
    ggplot(aes(x = x)) +
    geom_dots(layout = layout, side = side, stackratio = if (layout == "hex") 0.9 else 1) +
    labs(
      subtitle = paste0("layout = ", deparse(layout), if (layout == "hex") " with stackratio = 0.9"),
      x = NULL,
      y = NULL
    ) +
    scale_y_continuous(breaks = NULL) +
    theme(panel.border = element_rect(color = "gray75", fill = NA))
}

(layout_plot("bin", side = "top") + layout_plot("hex", side = "top")) /
  (layout_plot("weave", side = "top") + layout_plot("swarm", side = "top")) +
  plot_annotation(title = 'geom_dots() layouts with side = "top"')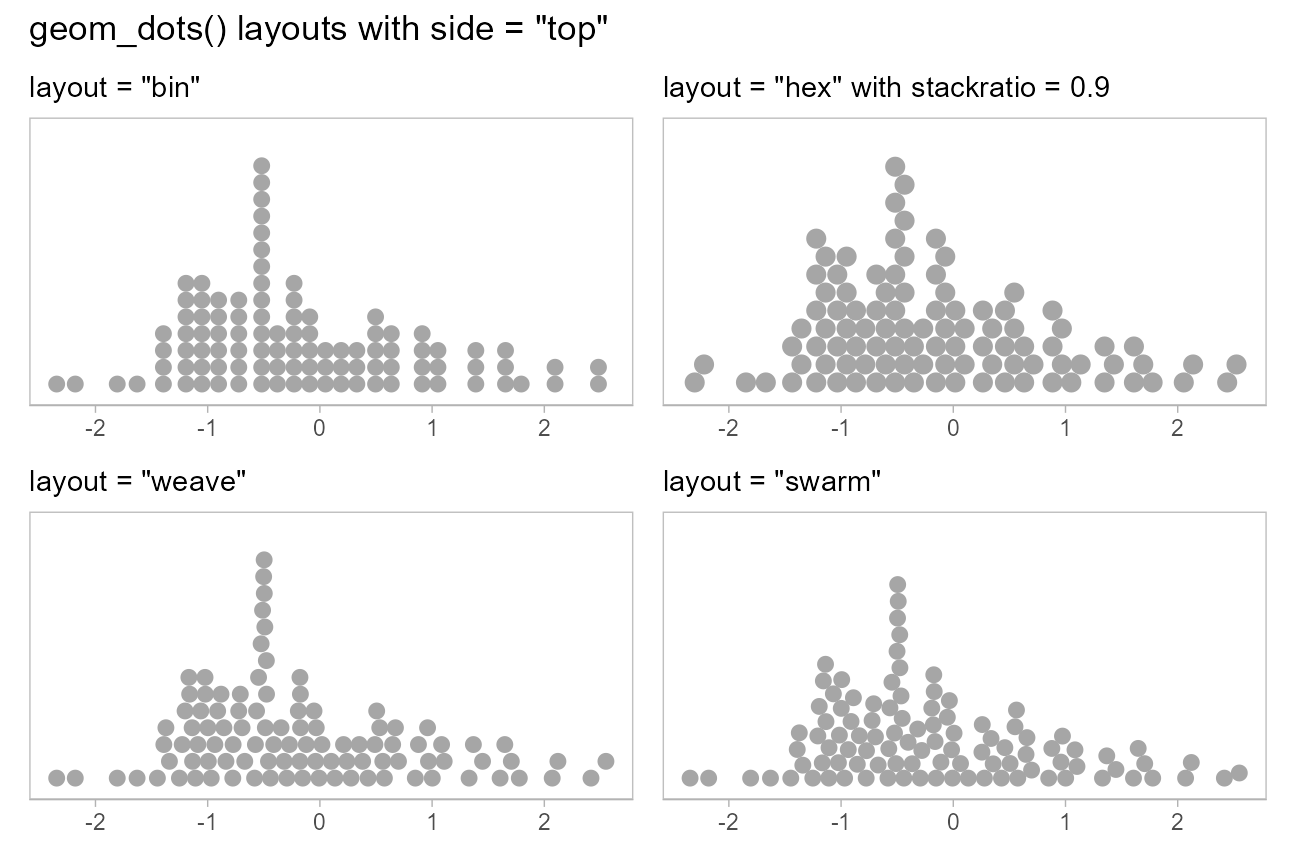

When side is "both", these layouts look like this:

(layout_plot("bin", side = "both") + layout_plot("hex", side = "both")) /
  (layout_plot("weave", side = "both") + layout_plot("swarm", side = "both")) +
  plot_annotation(title = 'geom_dots() layouts with side = "both"')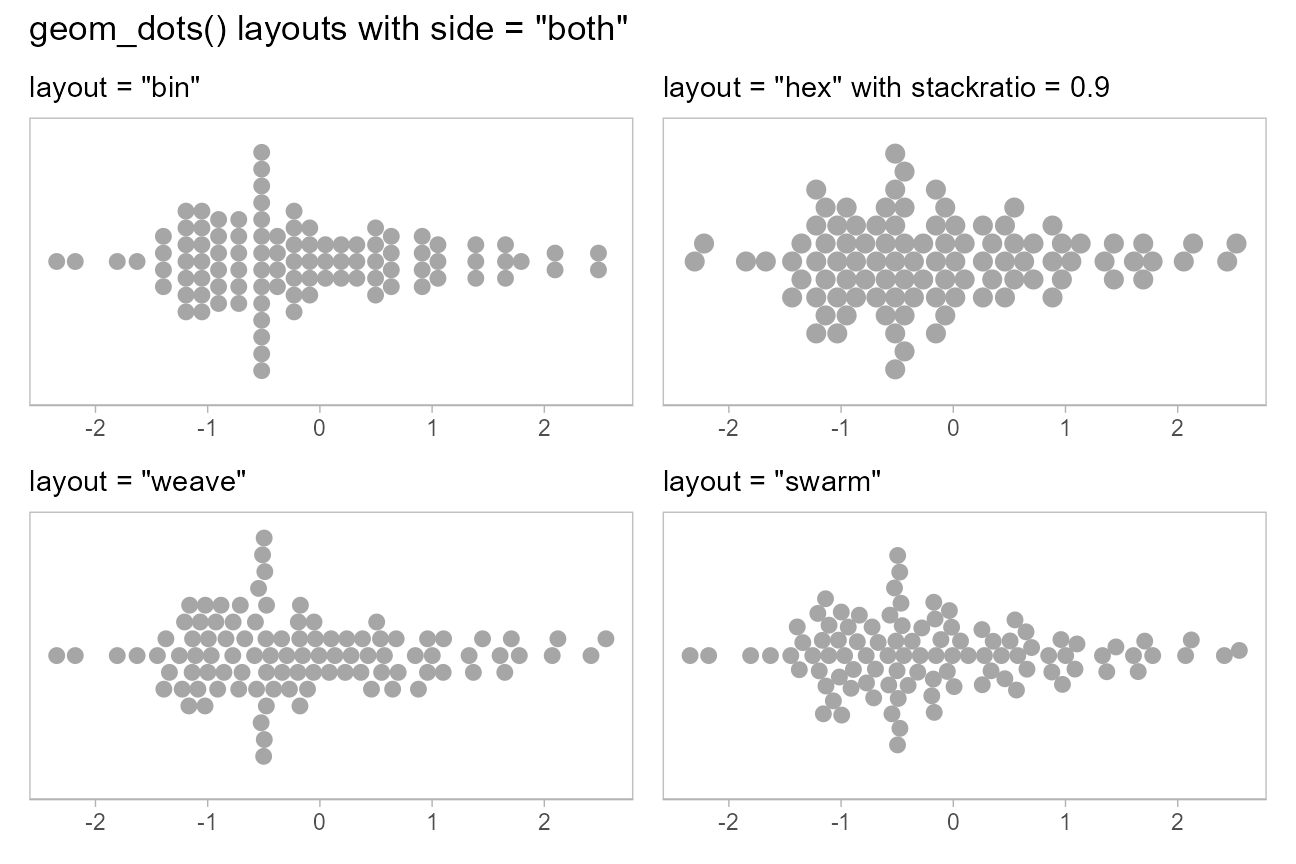

Beeswarm plots

Thus, it is possible to create beeswarm plots by using geom_dots() with side = "both":

set.seed(1234)

abc_df = tibble(
  value = rnorm(300, mean = c(1,2,3), sd = c(1,2,2)),
  abc = rep(c("a", "b", "c"), 100)
)

abc_df %>%
  ggplot(aes(x = abc, y = value)) +
  geom_dots(side = "both") +
  ggtitle('geom_dots(side = "both")')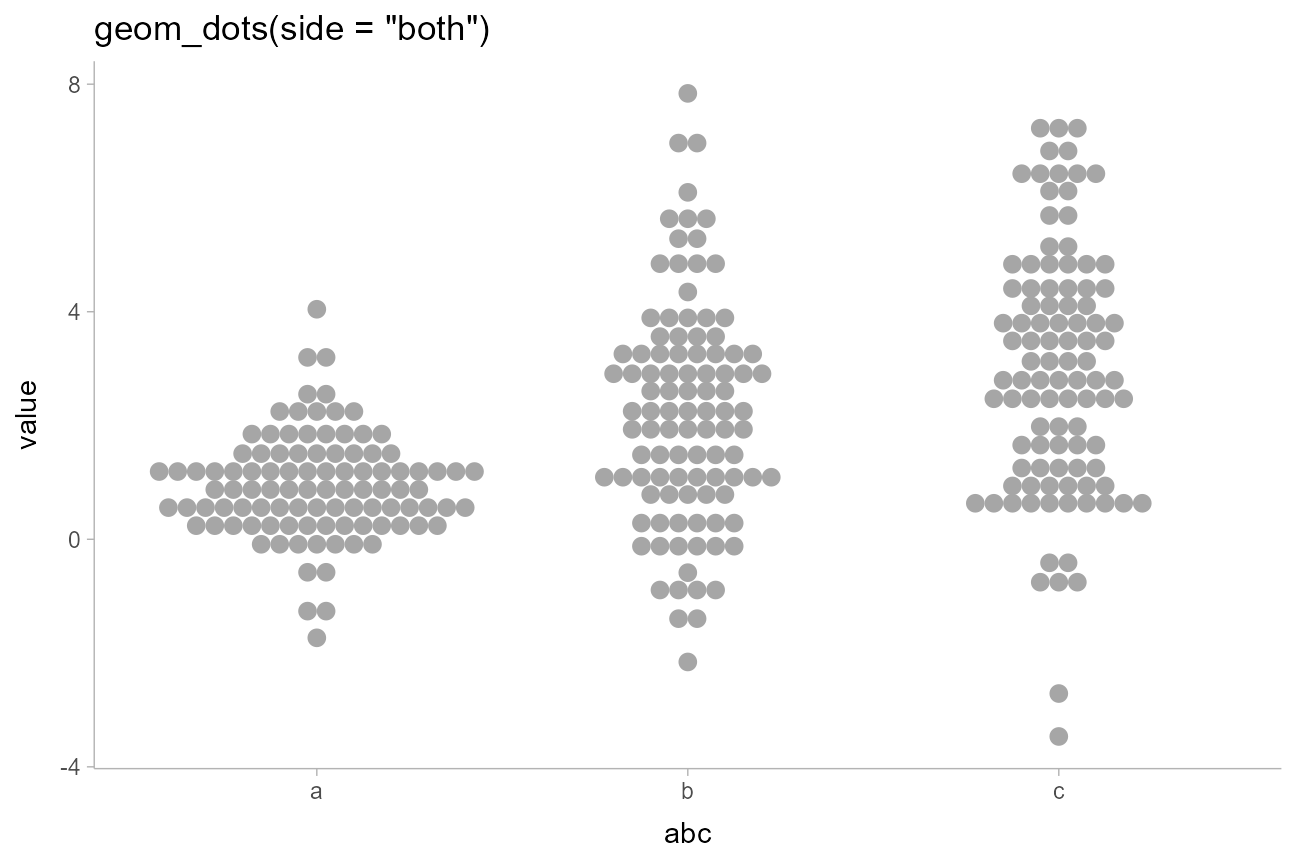

side = "both" also tends to work well with the "hex" and "swarm" layouts for more classic-looking “beeswarm” plots:

abc_df %>%
  ggplot(aes(x = abc, y = value)) +
  geom_dots(side = "both", layout = "hex", stackratio = 0.92) +
  ggtitle('geom_dots(side = "both", layout = "hex")')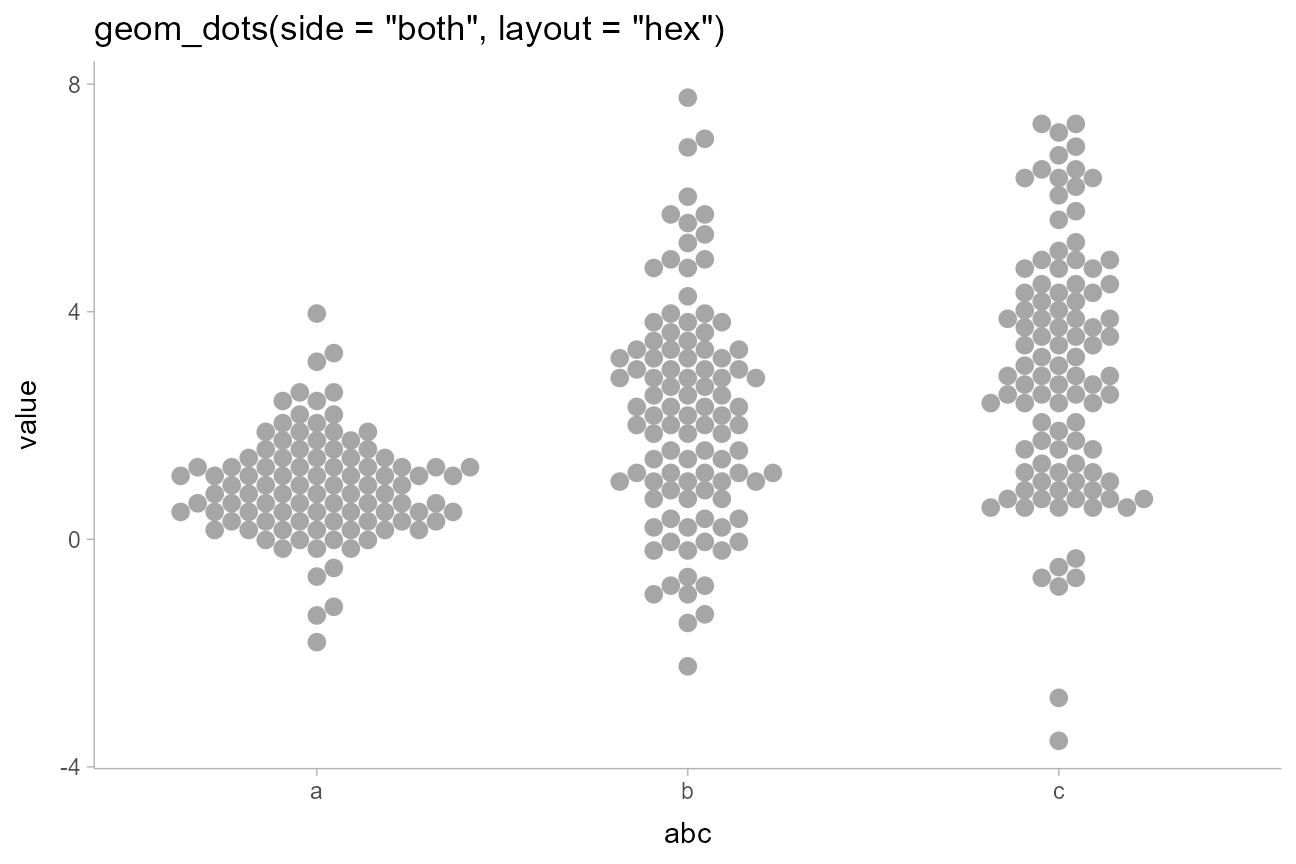

The combination of binwidth = unit(1.5, "mm") and overflow = "compress" (see the section on large samples, below) can be used to set the dot size to a specific size while guaranteeing the layout stays within the bounds of the geom. This combination is used by two shortcut geoms, geom_swarm() and geom_weave(), which use the "swarm" and "weave" layouts respectively. These also use side = "both", and are intended to make it easy to create good-looking beeswarm plots without manually tweaking settings:

set.seed(1234)

swarm_data = tibble(
  y = rnorm(300, c(1,4)),
  g = rep(c("a","b"), 150)
)

swarm_plot = swarm_data %>%
  ggplot(aes(x = g, y = y)) +
  geom_swarm(linewidth = 0, alpha = 0.75) +
  labs(title = "geom_swarm()")

weave_plot = swarm_data %>%
  ggplot(aes(x = g, y = y)) +
  geom_weave(linewidth = 0, alpha = 0.75) +
  labs(title = "geom_weave()")

swarm_plot + weave_plot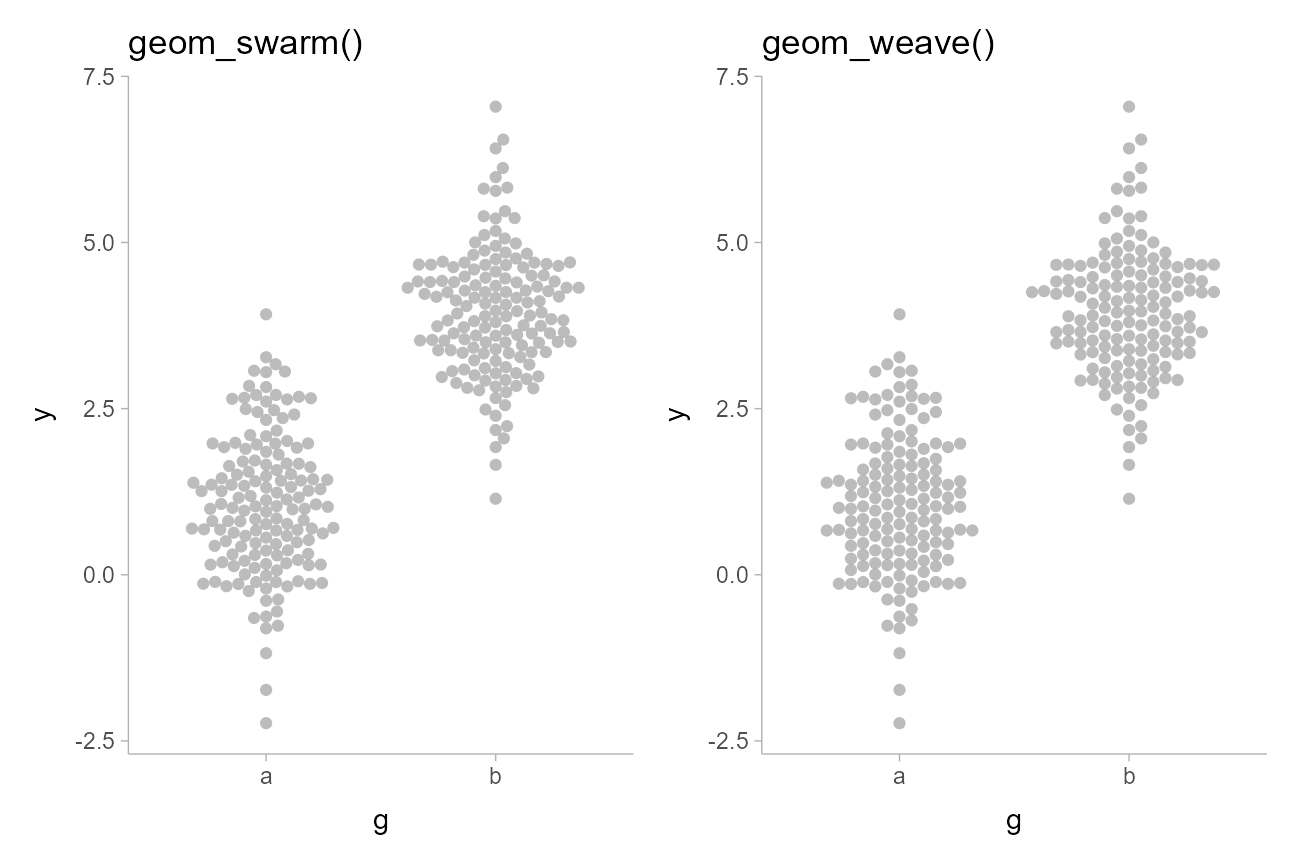

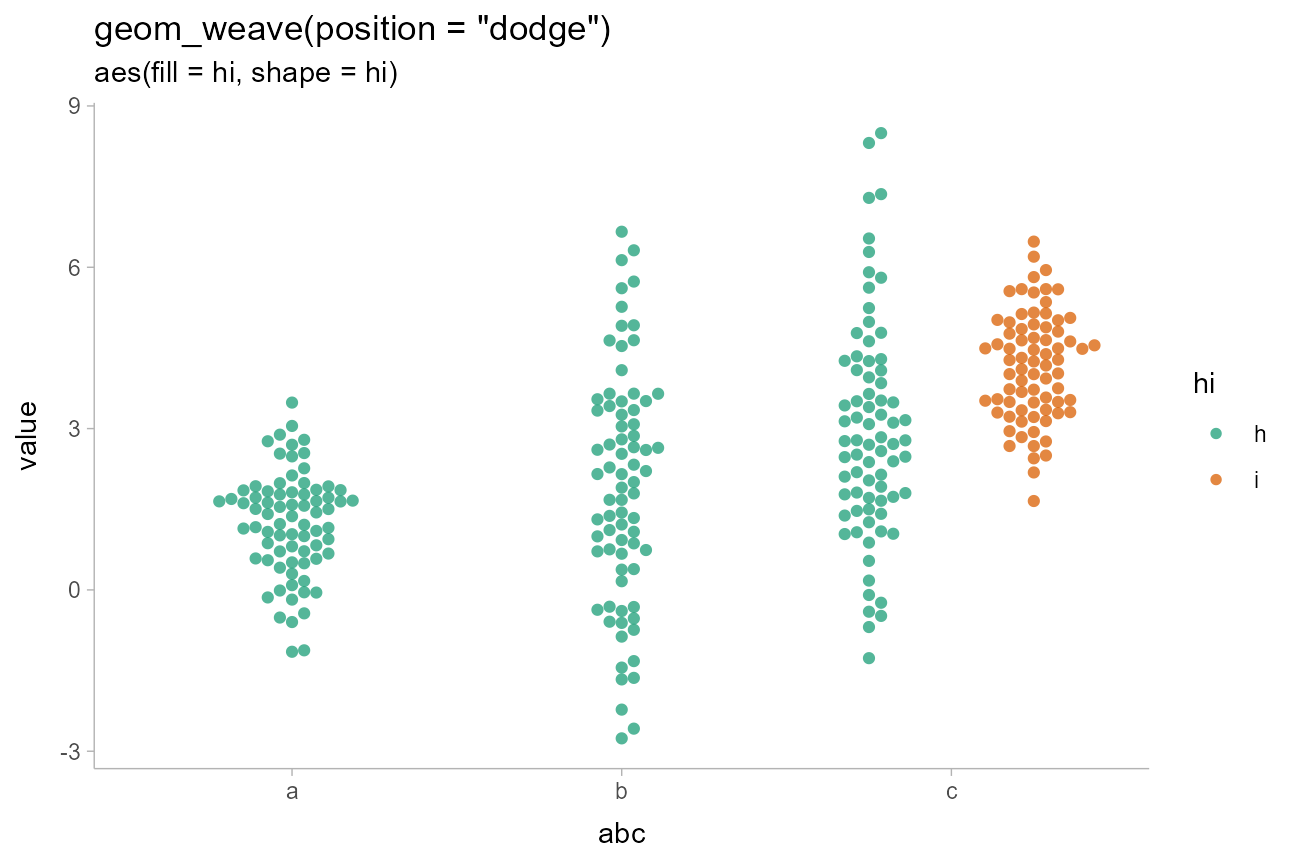
Varying `color`, `fill`, `shape`, and `linewidth`

Aesthetics like color, fill, shape, and linewidth can be varied over the dots. For example, we can vary the fill aesthetic to create two subgroups, and use position = "dodge" to dodge entire “swarms” at once so the subgroups do not overlap. We’ll also set linewidth = 0 so that the default gray outline is not drawn:

set.seed(12345)

abcc_df = tibble(
  value = rnorm(300, mean = c(1,2,3,4), sd = c(1,2,2,1)),
  abc = rep(c("a", "b", "c", "c"), 75),
  hi = rep(c("h", "h", "h", "i"), 75)
)

abcc_df %>%
  ggplot(aes(y = value, x = abc, fill = hi)) +
  geom_weave(position = "dodge", linewidth = 0, alpha = 0.75) +
  scale_fill_brewer(palette = "Dark2") +
  ggtitle(
    'geom_weave(position = "dodge")',
    'aes(fill = hi, shape = hi)'
  )

Varying discrete aesthetics within dot groups

By default, if you assign a discrete variable to fill, color,shape, etc it will also be used in thegroup` aesthetic to determine dot groups, which are laid out separate (and can be dodged separately, as above).

If you override this behavior by setting group to NA (or to some other variable you want to group dot layouts by), geom_dotsinterval() will leave dots in data order within the layout but allow aesthetics to vary across them.

For example:

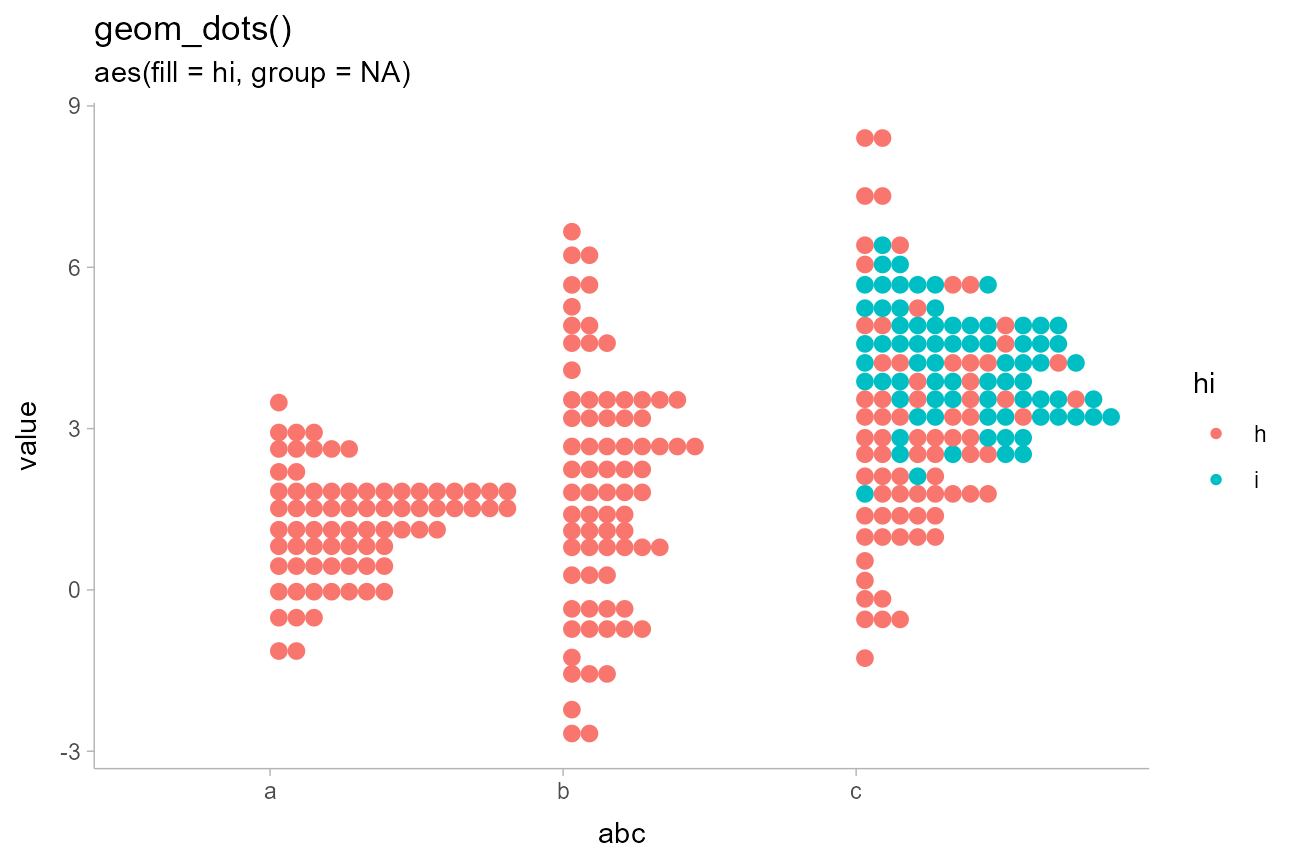
abcc_df %>%
  ggplot(aes(y = value, x = abc, fill = hi, group = NA)) +
  geom_dots(linewidth = 0) +
  scale_color_brewer(palette = "Dark2") +
  ggtitle(
    'geom_dots()',
    'aes(fill = hi, group = NA)'
  )

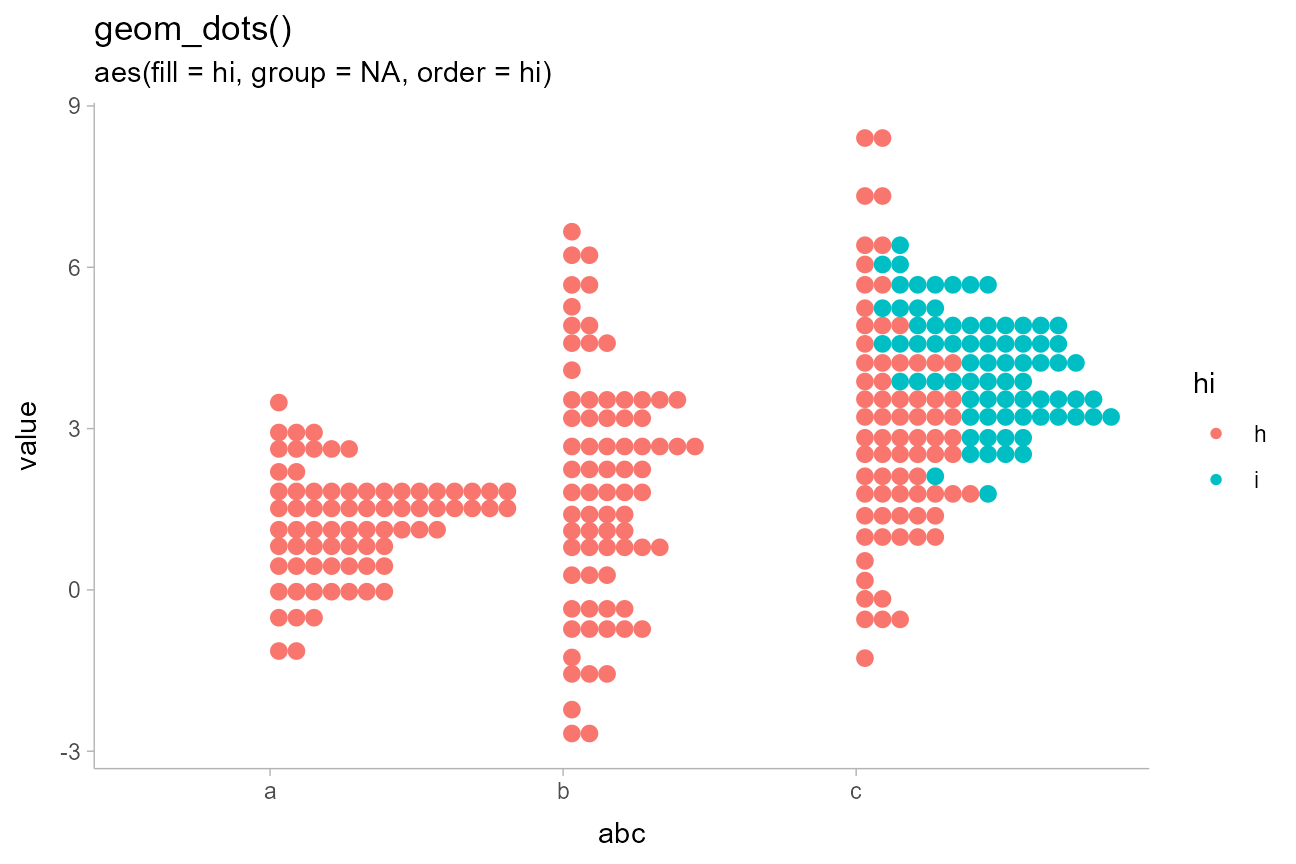
By default, dot positions within bins for the "bin" layout are determined by their data values (e.g. by the y values in the above chart). You can override this by passing a variable to the order aesthetic, which will set the sort order within bins. This can be used to create “stacked” dotplots by setting order to a discrete variable:

abcc_df %>%
  ggplot(aes(y = value, x = abc, fill = hi, group = NA, order = hi)) +
  geom_dots(linewidth = 0) +
  scale_color_brewer(palette = "Dark2") +
  ggtitle(
    'geom_dots()',
    'aes(fill = hi, group = NA, order = hi)'
  )

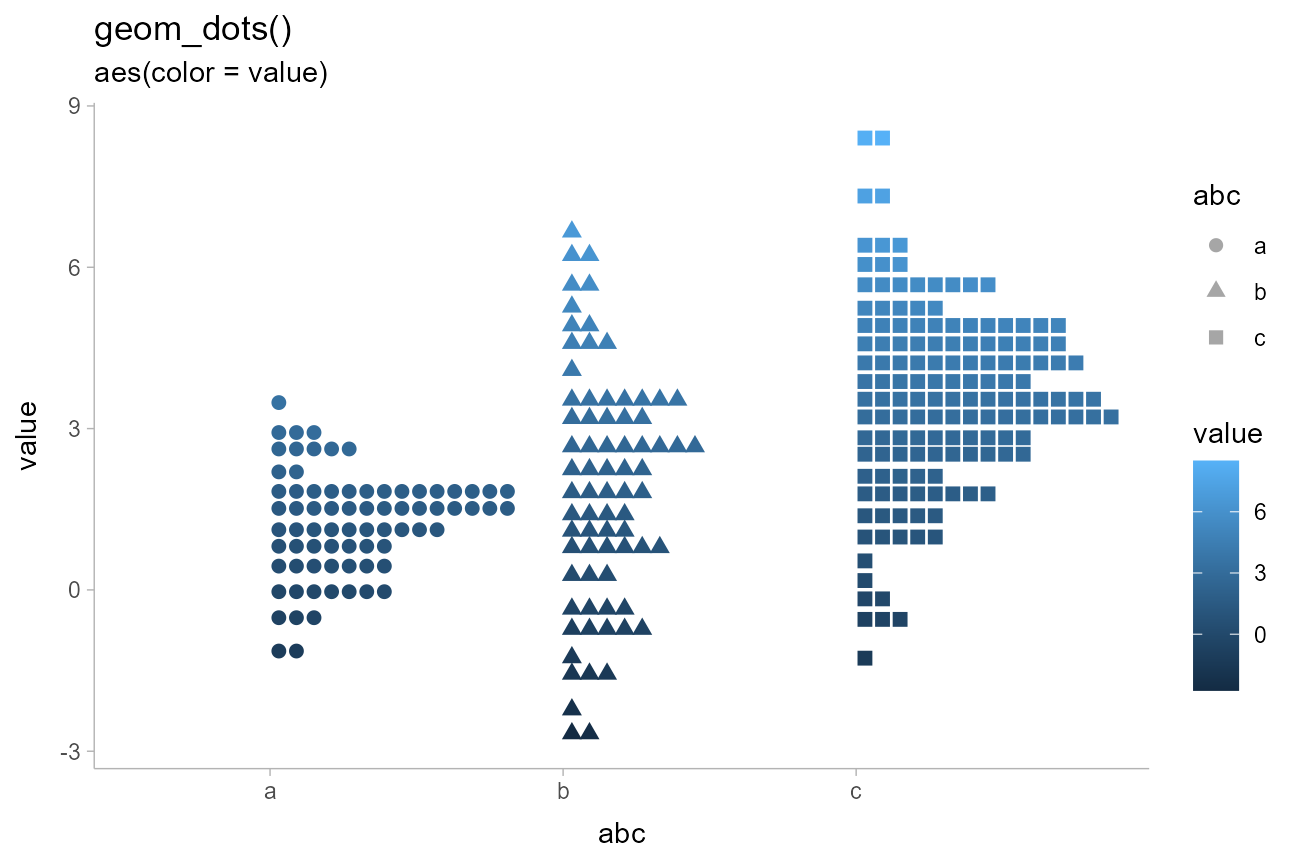
Varying continuous aesthetics within dot groups

Continuous variables can also be varied within groups. Since continuous variables will not automatically set the group aesthetic, we can simply assign them to the desired aesthetic we want to vary:

abcc_df %>%
  arrange(hi) %>%
  ggplot(aes(y = value, x = abc, shape = abc, color = value)) +
  geom_dots() +
  ggtitle(
    'geom_dots()',
    'aes(color = value)'
  )

Constraining dot size

When sample sizes can vary widely (and dynamically), it can be difficult to set a reasonable dot size that works on all charts. In this case, it can be useful to set constraints on the dot sizes picked by the automatic bin width selection algorithm.

For example, on very large samples, dots may become smaller than desired. Consider the following increasingly large samples:

set.seed(1234)

ns = c(50, 200, 500, 5000)
increasing_samples = data.frame(
  x = rgamma(sum(ns), 2, 2),
  n = rep(ns, ns)
)

increasing_samples %>%
  ggplot(aes(x = x)) +
  geom_dots() +
  facet_wrap(~ n) +
  labs(
    title = "geom_dots()",
    subtitle = "on large samples, dots may get too small"
  )

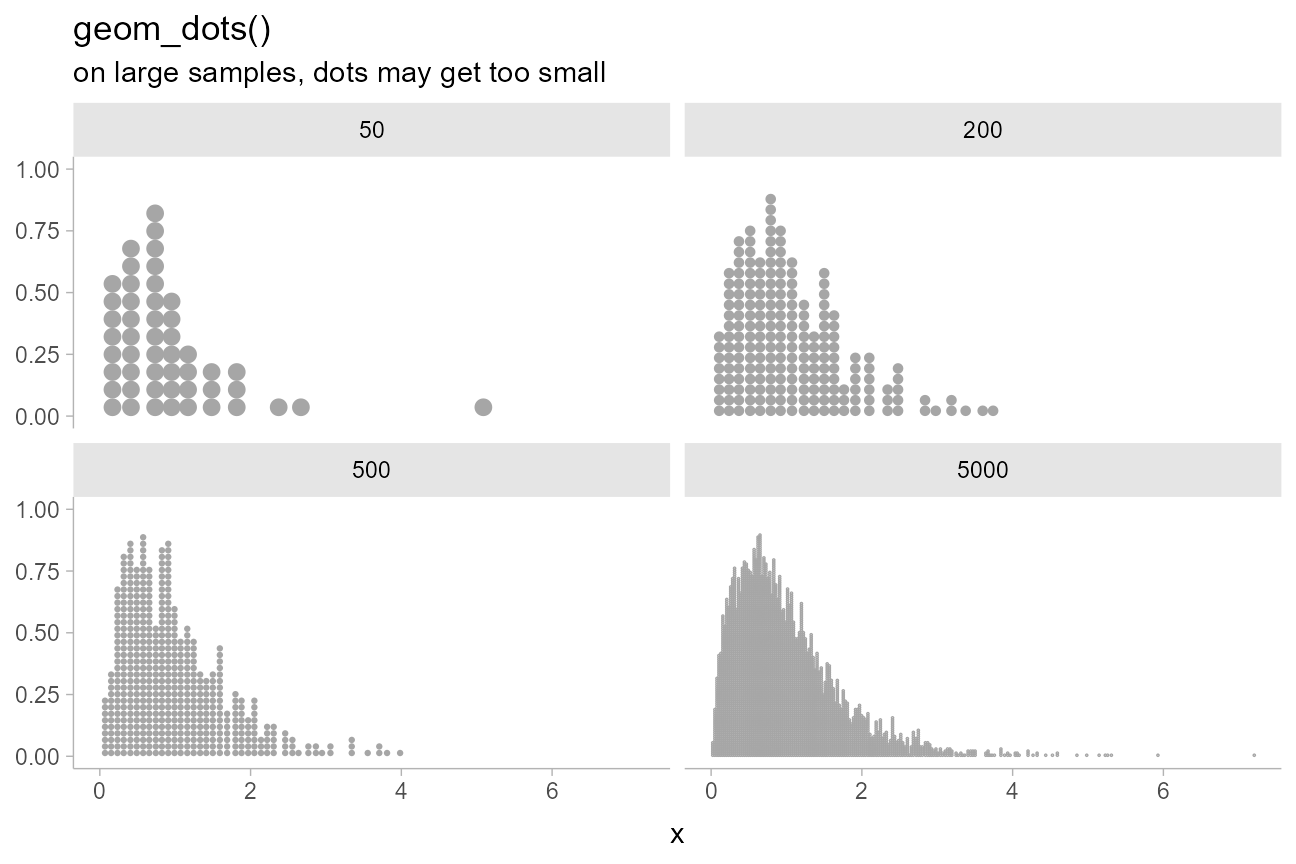
The dots become quite small on the 5000-dot dotplot, making it harder to read.

You can set constraints on the desired dot size / bin width by using the binwidth argument. To set a specific bin width, pass a single value; to set constraints, pass a length-2 vector, where the first element is the min and the second the max. The min can be 0 and the max can be Inf if you only want to constrain the other value (max or min, respectively). The bin width can be in data units (using numeric values) or in plotting units (using grid::unit()s).

For example, we could constrain the dot size to be greater than 1mm:

increasing_samples %>%
  ggplot(aes(x = x)) +
  geom_dots(binwidth = unit(c(1, Inf), "mm")) +
  facet_wrap(~ n) +
  labs(
    title = "geom_dots()",
    subtitle = 'binwidth = unit(c(1.5, Inf), "mm")'
  )

## Warning: The provided binwidth will cause dots to overflow the boundaries of the geometry.
## → Set `binwidth = NA` to automatically determine a binwidth that ensures dots fit within the
##   bounds,
## → OR set `overflow = "compress"` to automatically reduce the spacing between dots to ensure the
##   dots fit within the bounds,
## → OR set `overflow = "keep"` to allow dots to overflow the bounds of the geometry without producing
##   a warning.
## ℹ For more information, see the documentation of the `binwidth` and `overflow` arguments of
##   `?ggdist::geom_dots()` or the section on constraining dot sizes in vignette("dotsinterval")
##   (`vignette(ggdist::dotsinterval)`).
## The provided binwidth will cause dots to overflow the boundaries of the geometry.
## → Set `binwidth = NA` to automatically determine a binwidth that ensures dots fit within the
##   bounds,
## → OR set `overflow = "compress"` to automatically reduce the spacing between dots to ensure the
##   dots fit within the bounds,
## → OR set `overflow = "keep"` to allow dots to overflow the bounds of the geometry without producing
##   a warning.
## ℹ For more information, see the documentation of the `binwidth` and `overflow` arguments of
##   `?ggdist::geom_dots()` or the section on constraining dot sizes in vignette("dotsinterval")
##   (`vignette(ggdist::dotsinterval)`).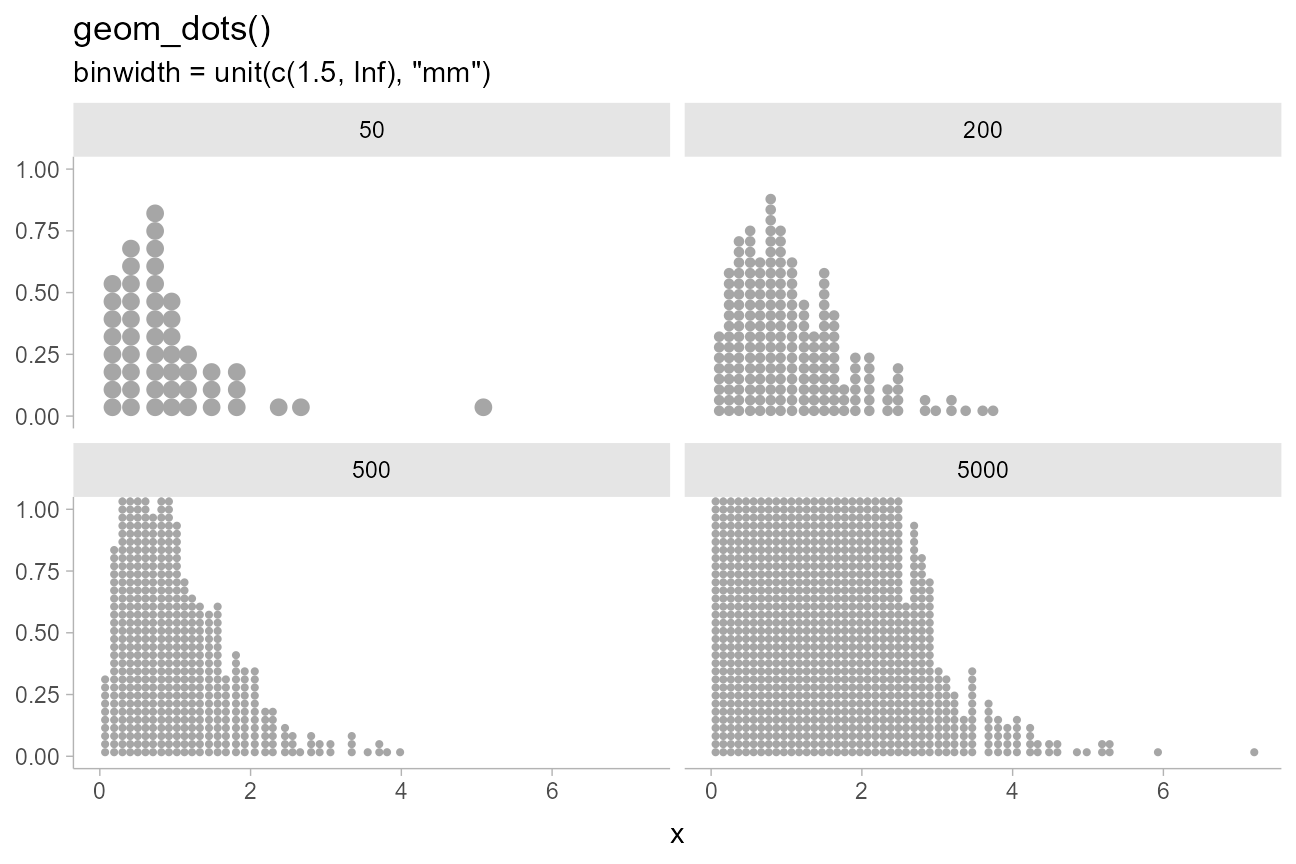

Notice how the dots now go off the page and we receive a warning with suggestions on how to fix the layout. If we set overflow = "compress", instead of overflowing, the layout will compress the spacing between dots to keep them within the geometry’s bounds:

increasing_samples %>%
  ggplot(aes(x = x)) +
  geom_dots(binwidth = unit(c(1, Inf), "mm"), overflow = "compress", alpha = 0.75) +
  facet_wrap(~ n) +
  labs(
    title = "geom_dots()",
    subtitle = 'binwidth = unit(c(1, Inf), "mm"), overflow = "compress"'
  )

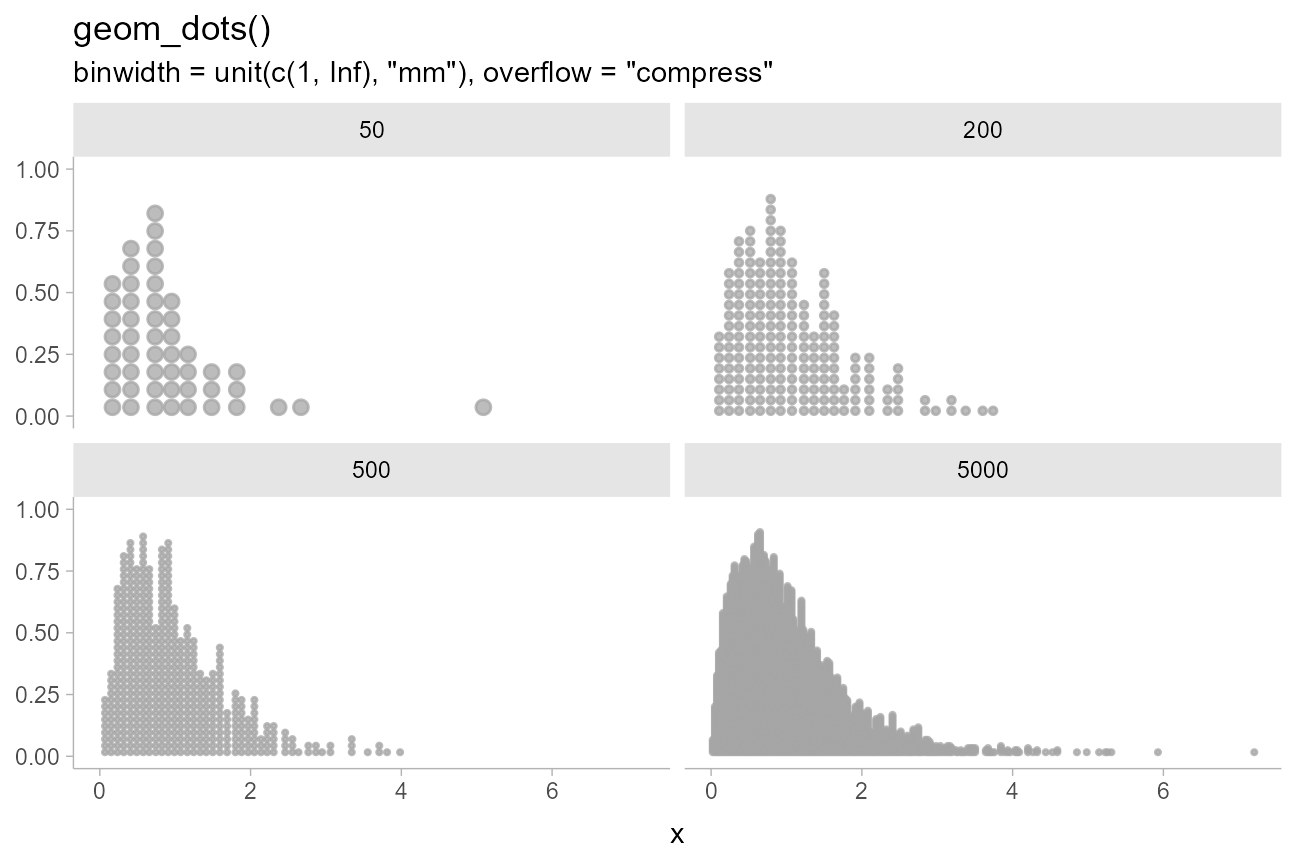
These settings give reasonable displays in small sample sizes and scale up to larger sample sizes without changing settings.

On discrete distributions

The dots family includes a variety of features to make visualizing discrete and categorical distributions easier. These distributions can be hard to visualize under the default settings if the dots become very small:

set.seed(1234)
abcd_df = tibble(
  x = sample(c("a", "b", "c", "d"), 1000, replace = TRUE, prob = c(0.27, 0.6, 0.03, 0.005)),
  g = rep(c("a","b"), 500)
)

abcd_df %>%
  ggplot(aes(x = x)) +
  geom_dots() +
  scale_y_continuous(breaks = NULL) +
  labs(
    title = "geom_dots()",
    subtitle = "on a large discrete sample"
  )

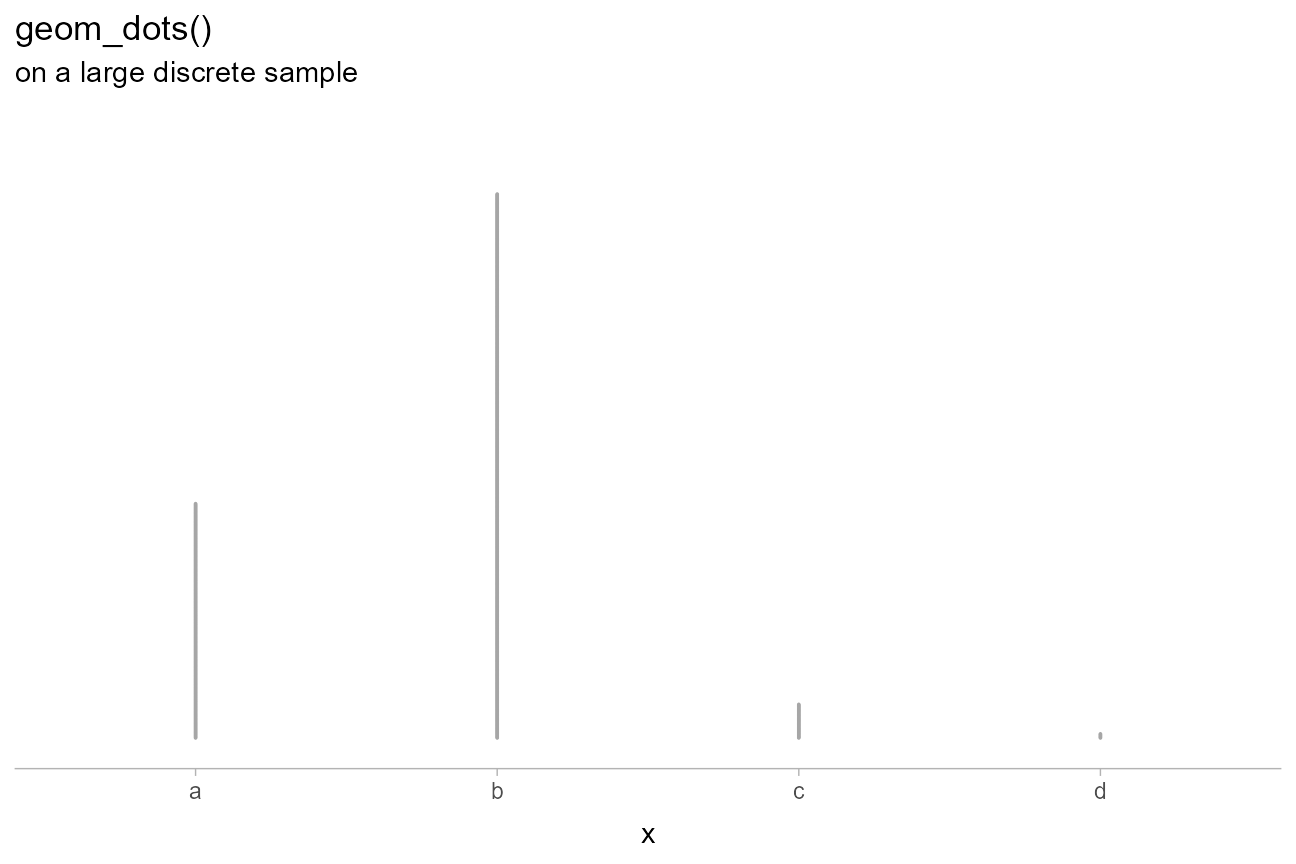
The automatic bin width algorithm selects a dot size that is very small in order to ensure the tallest bin fits in the plot, but this means the dots are hard to see.

Bar-like layouts can be achieved by using layout = "bar":

abcd_df %>%
  ggplot(aes(x = x, fill = g, order = g)) +
  geom_dots(layout = "bar", group = NA, color = NA) +
  scale_y_continuous(breaks = NULL) +
  labs(
    title = 'geom_dots(aes(fill = g), layout = "bar", group = NA)',
    subtitle = "on a large discrete sample"
  )

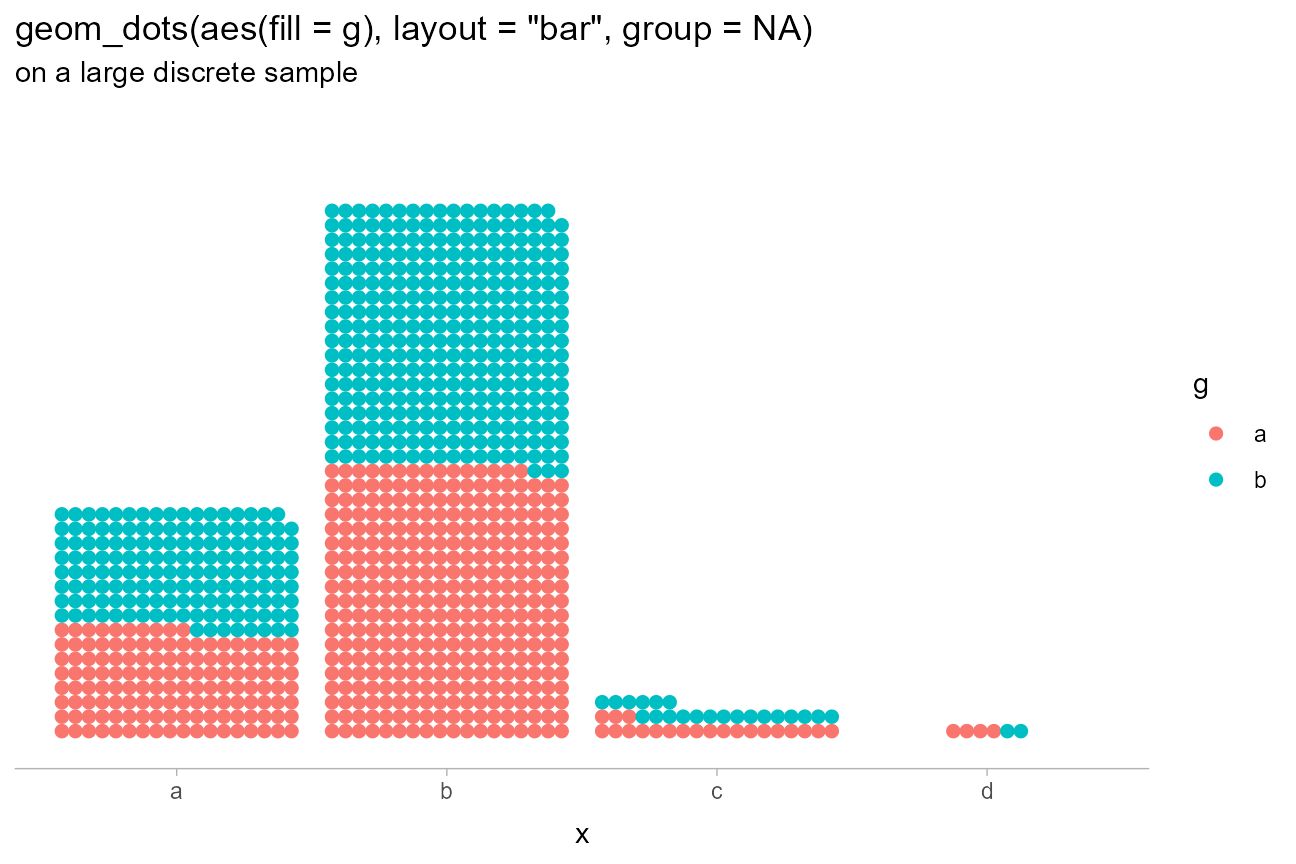
Notice how we set group = NA to override the default ggplot2 behavior of grouping data by all discrete variables. This allows the layout to be calculated taking all groups into account.

We can also use the smooth parameter to improve the display of discrete distributions, for which geom_dots() supports a handful of smoothers. These all correspond to functions that start with smooth_, like smooth_bounded(), smooth_unbounded(), and smooth_discrete(), and can be applied either by passing the suffix as a string (e.g. smooth = "bounded") or by passing the function itself, to set specific options on it (e.g. smooth = smooth_bounded(adjust = 0.5)).

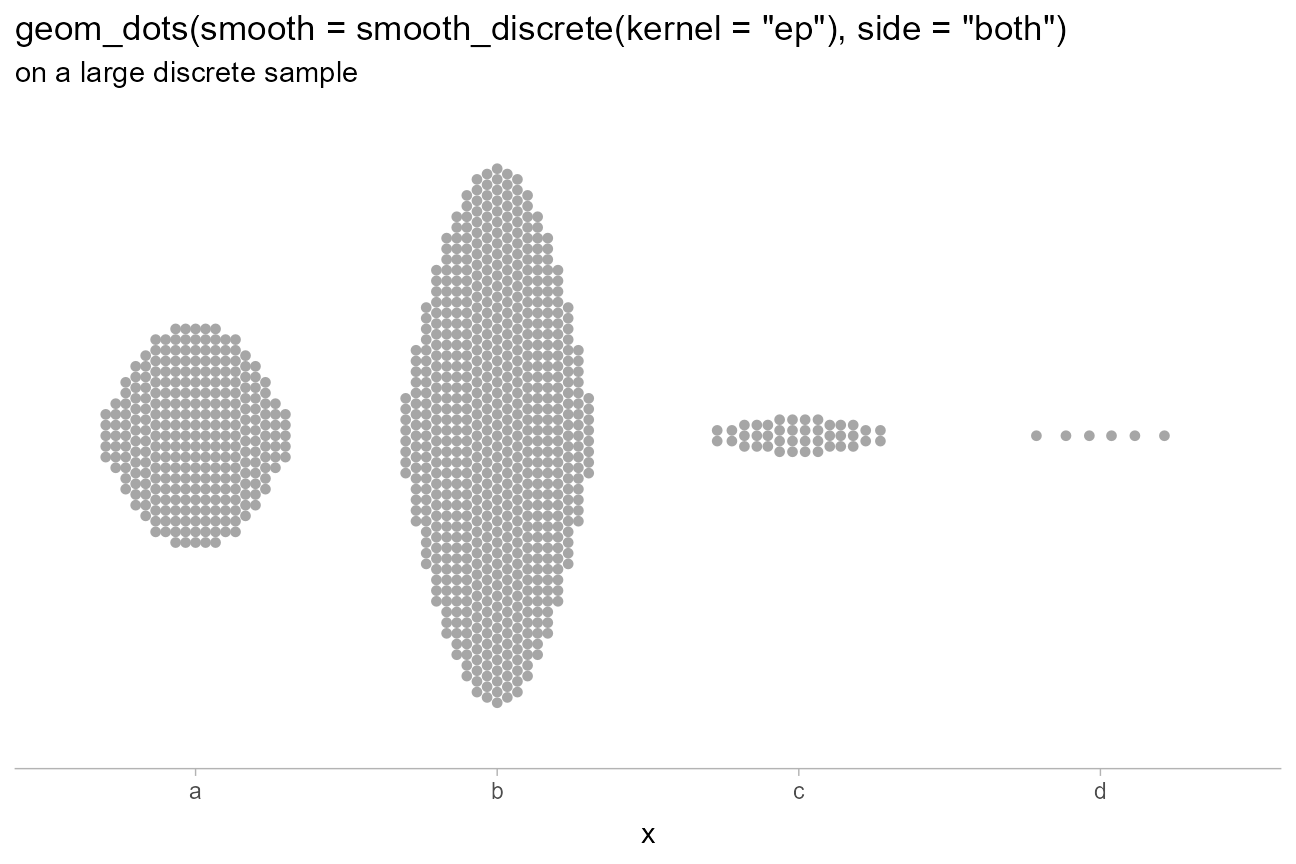
smooth_discrete() applies a kernel density smoother whose default bandwidth is less than the distances between bins. We can use the kernel argument (passed to density_bounded(); the same kernels from stats::density() are available) to change the shape of the bins.

For example, using the "epanechnikov" (parabolic) kernel along with side = "both", we can create lozenge-like shapes. We’ll abbreviate the kernel "ep" to save typing out "epanechnikov" (partial matching is allowed):

abcd_df %>%
  ggplot(aes(x = x)) +
  geom_dots(smooth = smooth_discrete(kernel = "ep"), side = "both") +
  scale_y_continuous(breaks = NULL) +
  labs(
    title = 'geom_dots(smooth = smooth_discrete(kernel = "ep"), side = "both")',
    subtitle = "on a large discrete sample"
  )

On analytical distributions

Like the stat_slabinterval() family, stat_dotsinterval() and stat_dots() support using both sample data (via x and y aesthetics) or analytical distributions (via the xdist and ydist aesthetics). For analytical distributions, these stats accept specifications for distributions in one of two ways:

Using distribution names as character vectors: this format uses aesthetics as follows:
- xdist, ydist, or dist: the name of the distribution, following R’s naming scheme. This is a string which should have "p", "q", and "d" functions defined for it: e.g., “norm” is a valid distribution name because the pnorm(), qnorm(), and dnorm() functions define the CDF, quantile function, and density function of the Normal distribution.
- args or arg1, … arg9: arguments for the distribution. If you use args, it should be a list column where each element is a list containing arguments for the distribution functions; alternatively, you can pass the arguments directly using arg1, … arg9.
Using distribution vectors from the distributional package or posterior::rvar() objects: this format uses aesthetics as follows:
- xdist, ydist, or dist: a distribution vector or posterior::rvar() produced by functions such as distributional::dist_normal(), distributional::dist_beta(), posterior::rvar_rng(), etc.

For example, here are a variety of distributions:

dist_df = tibble(
  dist = c(dist_normal(1,0.25), dist_beta(3,3), dist_gamma(5,5)),
  dist_name = format(dist)
)

dist_df %>%
  ggplot(aes(y = dist_name, xdist = dist)) +
  stat_dotsinterval(subguide = 'integer') +
  ggtitle(
    "stat_dotsinterval(subguide = 'integer')",
    "aes(y = dist_name, xdist = dist)"
  )

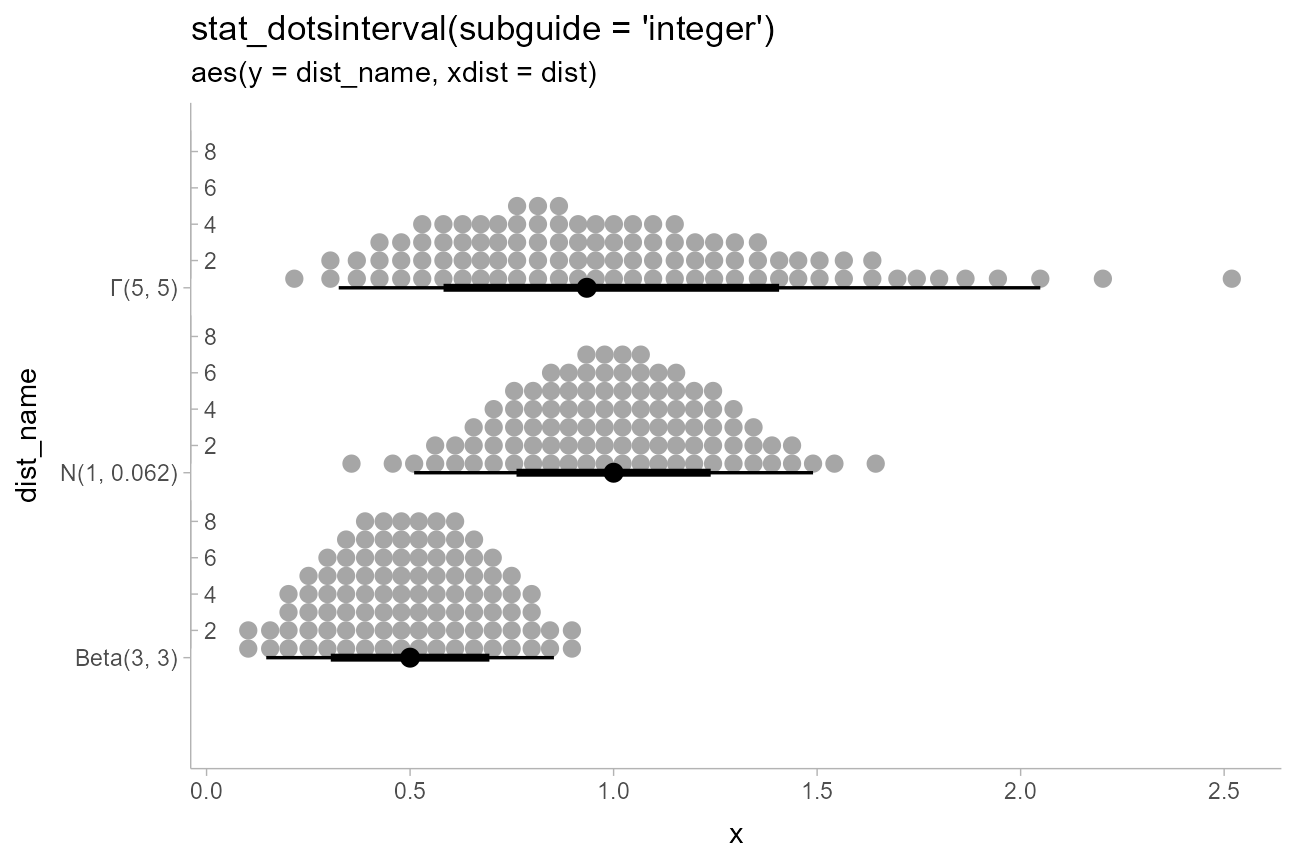
This example also shows the use of sub-guides to label dot counts. See the documentation of subguide_axis() and its shortcuts (particularly subguide_integer() and subguide_count()) for more examples.

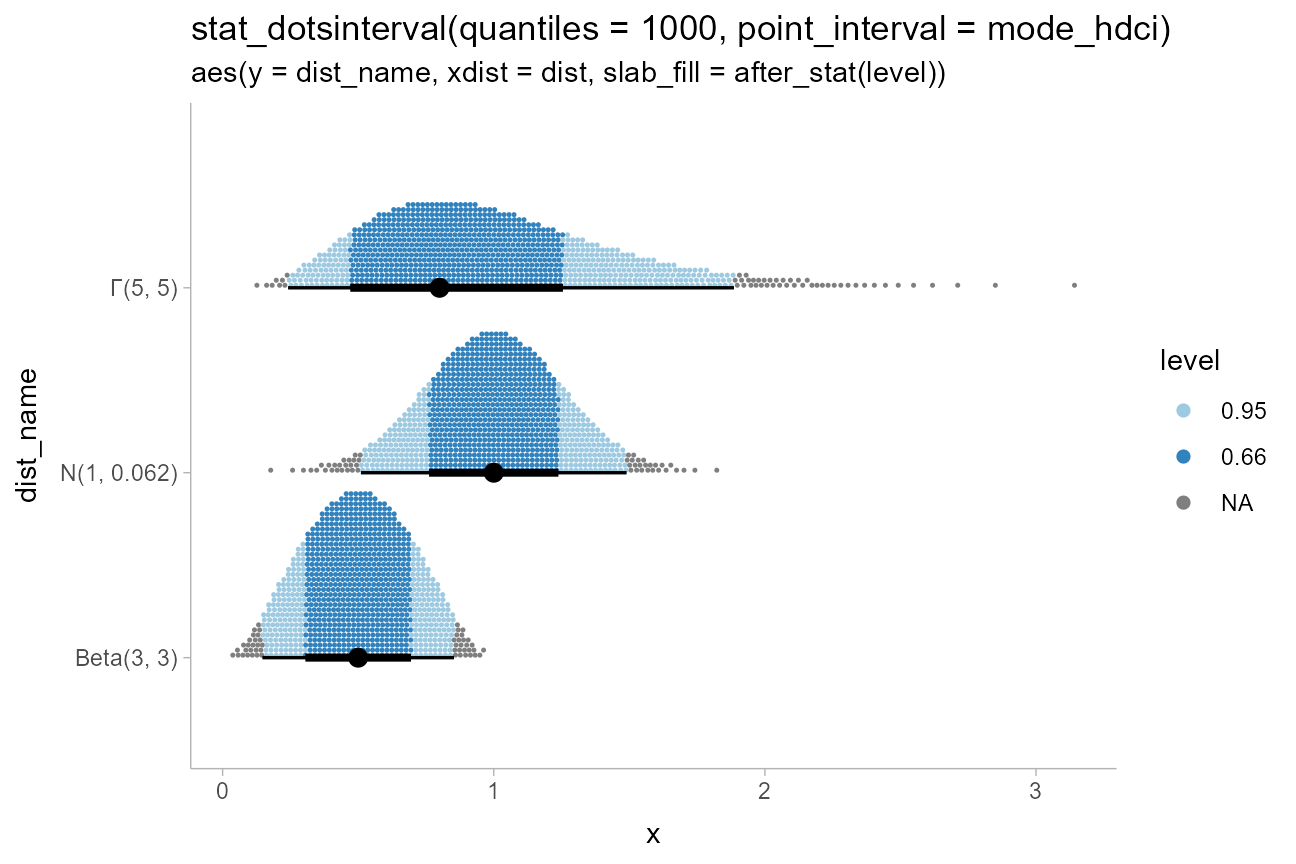
Analytical distributions are shown by default using 100 quantiles, sometimes referred to as a quantile dotplot, which can help people make better decisions under uncertainty (Kay 2016, Fernandes 2018). This can be changed using the quantiles argument. For example, we can plot the same distributions again using 1000 quantiles. We’ll also make use of point_interval to plot the mode and highest-density continuous intervals (instead of the default median and quantile intervals; see point_interval()).

We’ll also highlight some intervals by coloring the dots. Like with the stat_slabinterval() family, computed variables from the interval sub-geometry (level and .width) are available to the dots/slab sub-geometry, and correspond to the smallest interval containing that dot. We can use these to color dots according to the interval containing them (we’ll also use the "weave" layout since it maintains x positions better than the "bin" layout):

dist_df %>%
  ggplot(aes(y = dist_name, xdist = dist, slab_fill = after_stat(level))) +
  stat_dotsinterval(quantiles = 1000, point_interval = mode_hdci, layout = "weave", slab_color = NA) +
  scale_color_manual(values = scales::brewer_pal()(3)[-1], aesthetics = "slab_fill") +
  ggtitle(
    "stat_dotsinterval(quantiles = 1000, point_interval = mode_hdci)",
    "aes(y = dist_name, xdist = dist, slab_fill = after_stat(level))"
  )

When summarizing sample distributions with stat_dots()/stat_dotsinterval() (e.g. samples from Bayesian posteriors), one can also use the quantiles argument, though it is not on by default.

Varying continuous aesthetics with analytical distributions

While varying discrete aesthetics works similarly with stat_dotsinterval()/stat_dots() as it does with geom_dotsinterval()/geom_dots(), varying continuous aesthetics within dot groups typically requires mapping the continuous aesthetic after the stats are computed. This is because the stat (at least for analytical distributions) must first generate the quantiles before properties of those quantiles can be mapped to aesthetics.

Thus, because it relies upon generated variables from the stat, you can use the after_stat() or stage() functions from ggplot2 to map those variables. For example:

dist_df %>%
  ggplot(aes(y = dist_name, xdist = dist, slab_color = after_stat(x))) +
  stat_dotsinterval(slab_shape = 19, quantiles = 500) +
  scale_color_distiller(aesthetics = "slab_color", guide = "colorbar2") +
  ggtitle(
    "stat_dotsinterval(slab_shape = 19, quantiles = 500)",
    'aes(slab_color = after_stat(x)) +\nscale_color_distiller(aesthetics = "slab_color", guide = "colorbar2")'
  )

This example also demonstrates the use of sub-geometry scales: the slab_-prefixed aesthetics slab_color and slab_shape must be used to target the color and shape of the slab (“slab” here refers to the stack of dots) when using geom_dotsinterval() and stat_dotsinterval() to disambiguate between the point/interval and the dot stack. When using stat_dots()/geom_dots() this is not necessary.

Also note the use of scale_color_distiller(), a base ggplot2 color scale, with the slab_color aesthetic by setting the aesthetics and guide properties (the latter is necessary because the default guide = "colorbar" will not work with non-standard color aesthetics).

Thresholds

Another potentially useful application of post-stat aesthetic computation is to apply thresholds on a dotplot, coloring points on one side of a line differently. However, the default dotplot layout, "bin", can cause dots to be on the wrong side of a cutoff when coloring dots within dotplots. Thus it can be useful when plotting thresholds to use the "weave" or "swarm" layouts, which tend to position dots closer to their true x positions, rather than at bin centers:

ab_df = tibble(
  ab = c("a", "b"),
  mean = c(5, 7),
  sd = c(1, 1.5)
)

ab_df %>%
  ggplot(aes(y = ab, xdist = dist_normal(mean, sd), fill = after_stat(x < 6))) +
  stat_dots(position = "dodge", color = NA, layout = "weave") +
  labs(
    title = 'stat_dots(layout = "weave")',
    subtitle = "aes(fill = after_stat(x < 6))"
  ) +
  geom_vline(xintercept = 6, alpha = 0.25) +
  scale_x_continuous(breaks = 2:10)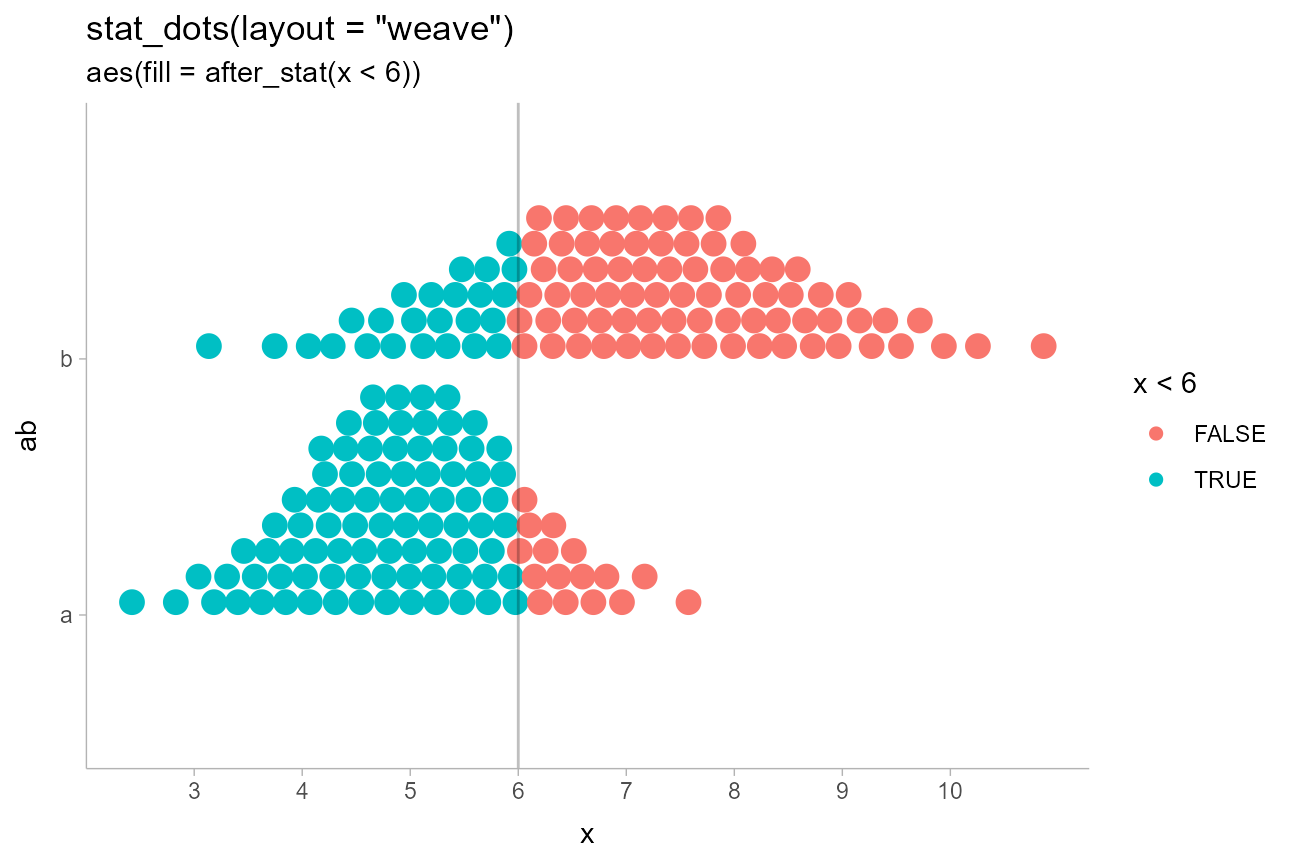

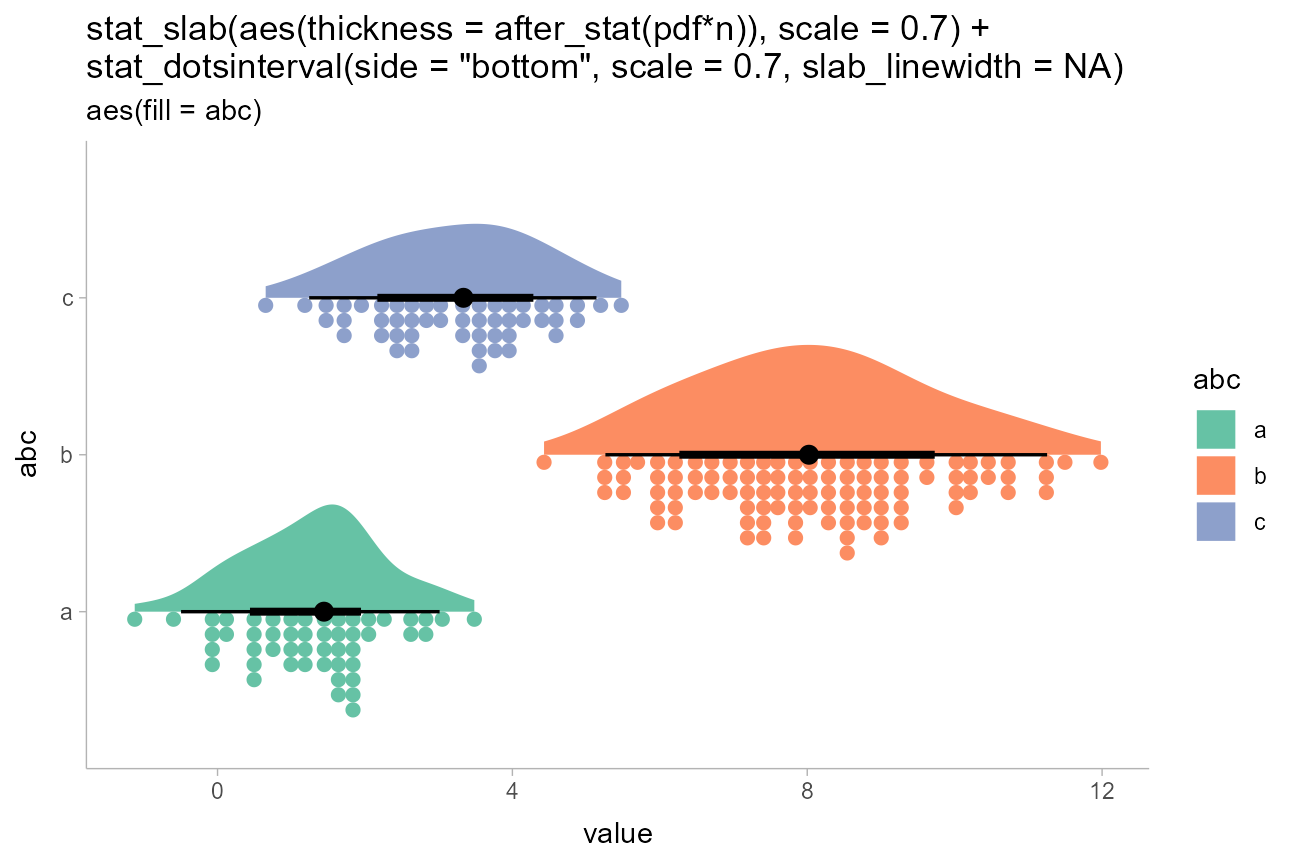
Rain cloud plots

Sometimes you may want to include multiple different types of slabs in the same plot in order to take advantage of the features each slab type provides. For example, people often combine densities with dotplots to show the underlying datapoints that go into a density estimate, creating so-called rain cloud plots.

To use multiple slab geometries together, you can use the side parameter to change which side of the interval a slab is drawn on and set the scale parameter to something around 0.5 (by default it is 0.9) so that the two slabs do not overlap. We’ll also scale the halfeye slab thickness by n (the number of observations in each group) so that the area of each slab represents sample size (and looks similar to the total area of its corresponding dotplot).

We’ll use a subsample of of the data to show how it might look on a reasonably-sized dataset.

set.seed(12345) # for reproducibility

tibble(
  abc = rep(c("a", "b", "b", "c"), 50),
  value = rnorm(200, c(1, 8, 8, 3), c(1, 1.5, 1.5, 1))
) %>%
  ggplot(aes(y = abc, x = value, fill = abc)) +
  stat_slab(aes(thickness = after_stat(pdf*n)), scale = 0.7) +
  stat_dotsinterval(side = "bottom", scale = 0.7, slab_linewidth = NA) +
  scale_fill_brewer(palette = "Set2") +
  ggtitle(
    paste0(
      'stat_slab(aes(thickness = after_stat(pdf*n)), scale = 0.7) +\n',
      'stat_dotsinterval(side = "bottom", scale = 0.7, slab_linewidth = NA)'
    ),
    'aes(fill = abc)'
  )

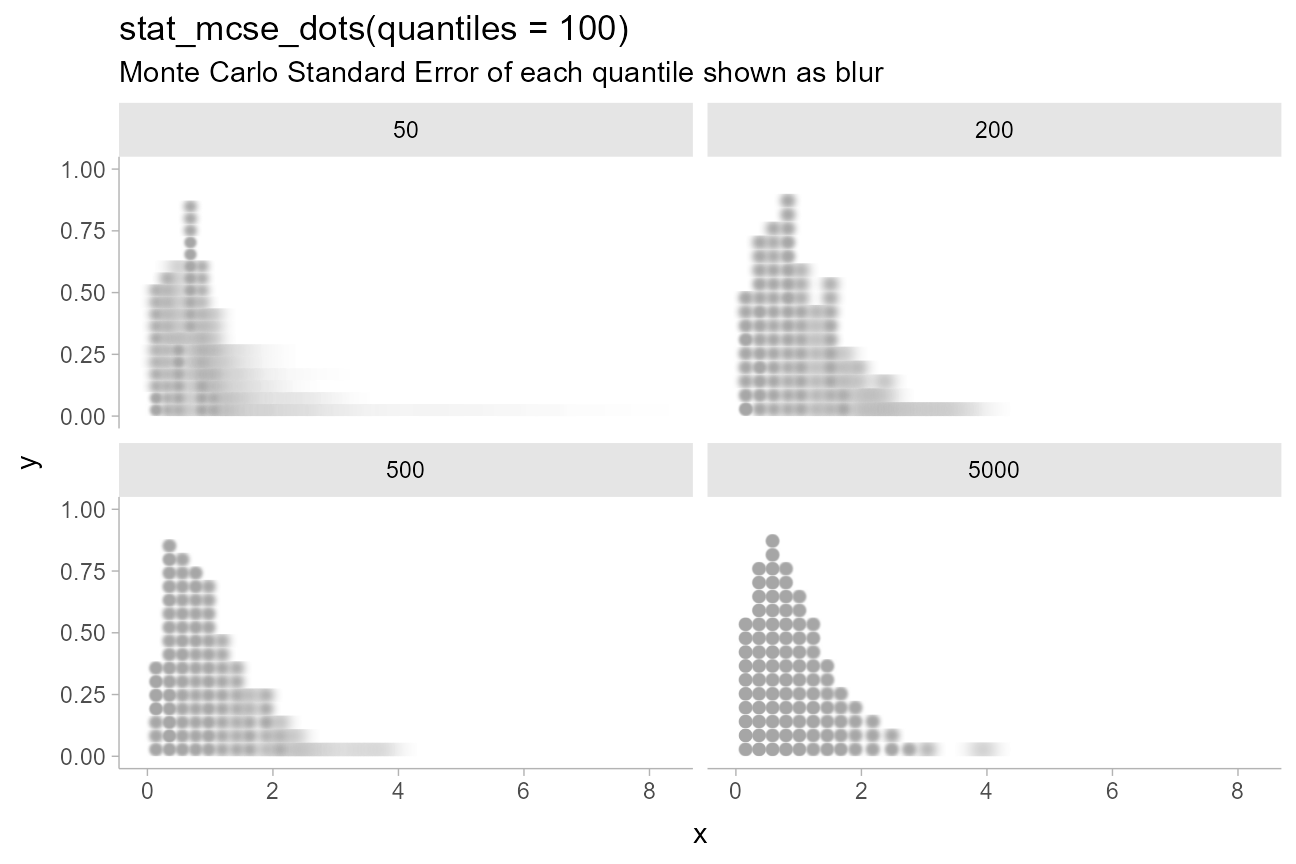
Dotplots with Monte Carlo Standard Error

A specialized variant of geom_dots(), geom_blur_dots(), supports visualizing dotplots with blur applied to each dot. stat_mcse_dots() uses geom_blur_dots() with posterior::mcse_quantile() to show the error in each quantile of a quantile dotplot:

increasing_samples %>%
  ggplot(aes(x = x)) +
  stat_mcse_dots(quantiles = 100) +
  facet_wrap(~ n) +
  labs(
    title = "stat_mcse_dots(quantiles = 100)",
    subtitle = "Monte Carlo Standard Error of each quantile shown as blur"
  )

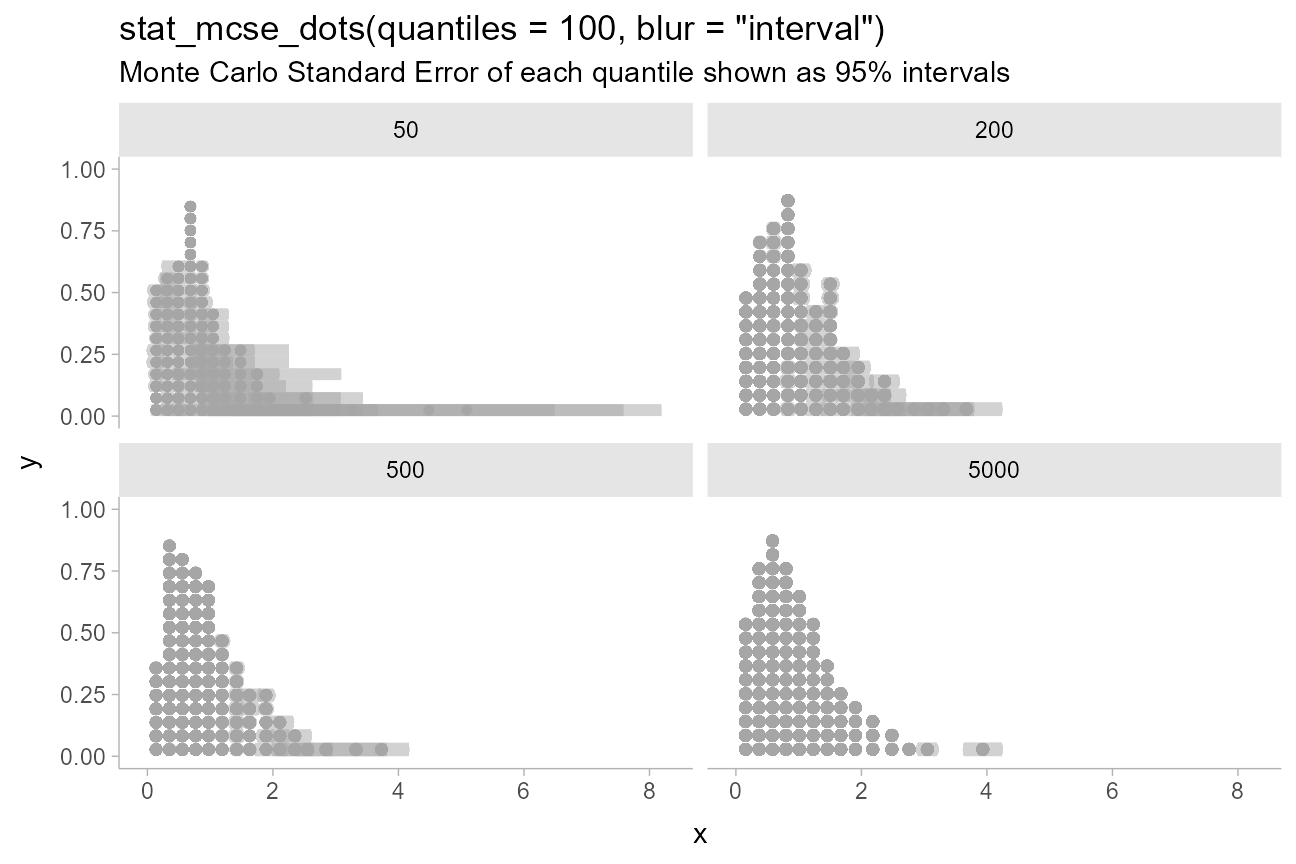
Custom blur functions can be selected using the blur parameter, including the built-in blur_interval(), which draws an interval with a default width of 95%:

increasing_samples %>%
  ggplot(aes(x = x)) +
  stat_mcse_dots(quantiles = 100, blur = "interval") +
  facet_wrap(~ n) +
  labs(
    title = 'stat_mcse_dots(quantiles = 100, blur = "interval")',
    subtitle = "Monte Carlo Standard Error of each quantile shown as 95% intervals"
  )

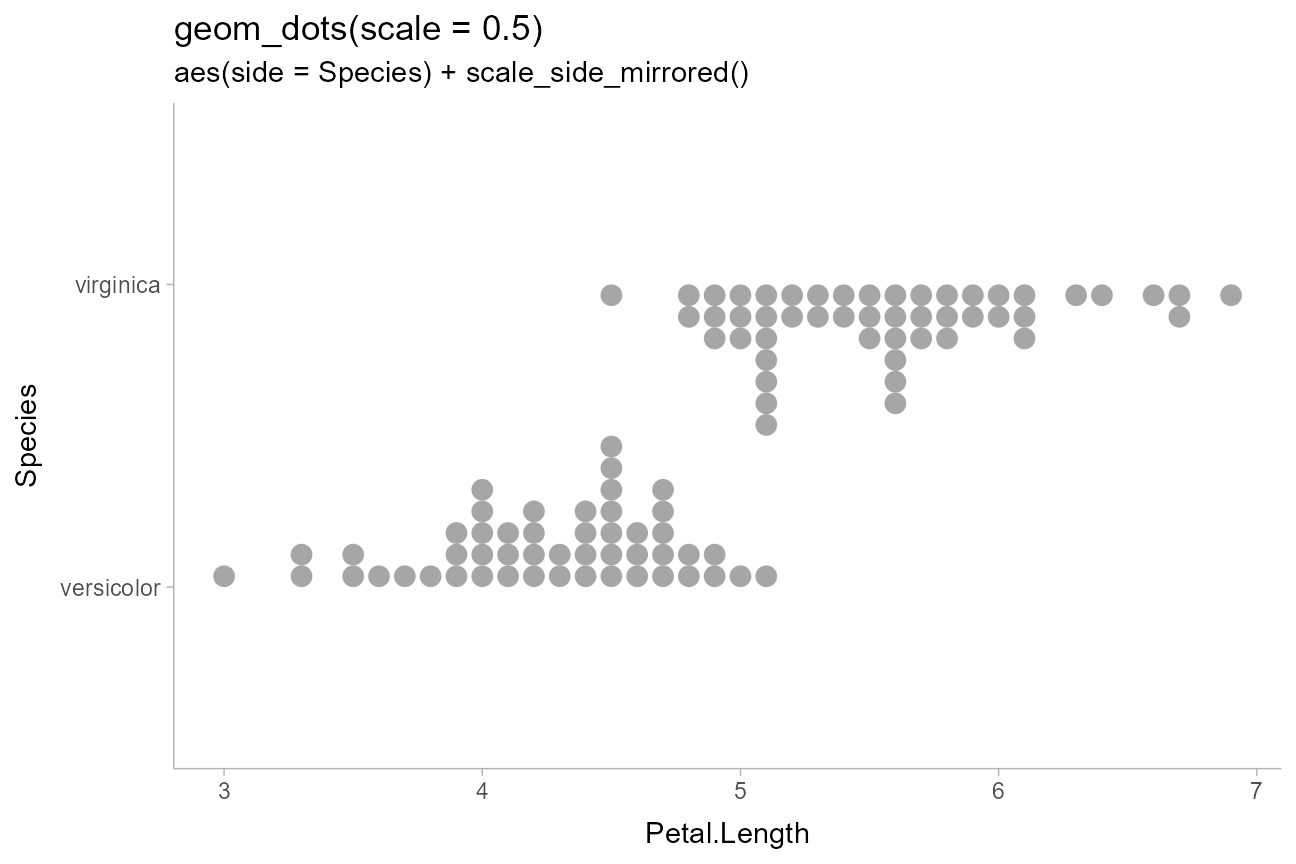
Logit dotplots

To demonstrate another useful plot type, the logit dotplot (courtesy Ladislas Nalborczyk), we’ll fit a logistic regression to some data on the petal length of the Iris versicolor and Iris virginica flowers.

First, we’ll demo varying the side aesthetic to create two dotplots that are “facing” each other: scale_side_mirrored() will set the side aesthetic to "top" or "bottom" if two categories are assigned to side“. We also adjust the scale so that the dots don’t overlap:

iris_v = iris %>%
  filter(Species != "setosa")

iris_v %>%
  ggplot(aes(x = Petal.Length, y = Species, side = Species)) +
  geom_dots(scale = 0.5) +
  scale_side_mirrored(guide = "none") +
  ggtitle(
    "geom_dots(scale = 0.5)",
    'aes(side = Species) + scale_side_mirrored()'
  )

This can also be accomplished by setting side directly and omitting scale_side_mirrored(); e.g. via aes(side = ifelse(Species == "virginica", "bottom", "top")).

Now we fit a logistic regression predicting species based on petal length:

m = glm(Species == "virginica" ~ Petal.Length, data = iris_v, family = binomial)
m

## 
## Call:  glm(formula = Species == "virginica" ~ Petal.Length, family = binomial, 
##     data = iris_v)
## 
## Coefficients:
##  (Intercept)  Petal.Length  
##      -43.781         9.002  
## 
## Degrees of Freedom: 99 Total (i.e. Null);  98 Residual
## Null Deviance:       138.6 
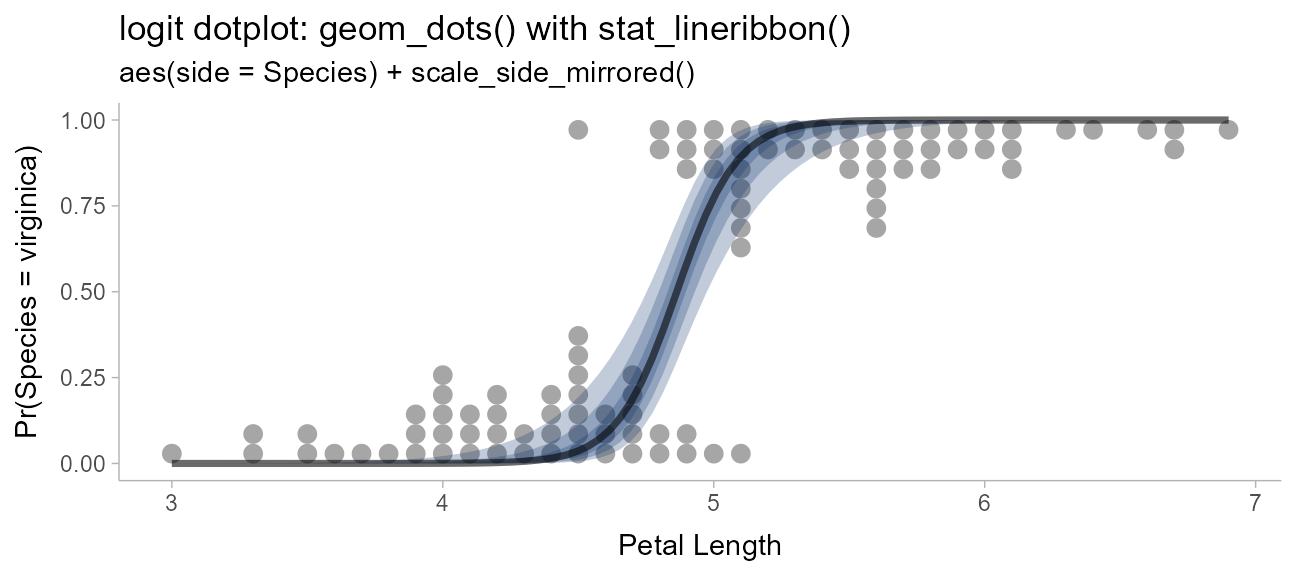
## Residual Deviance: 33.43     AIC: 37.43

Then we can overlay a fit line as a stat_lineribbon() (see vignette("lineribbon")) on top of the mirrored dotplots to create a logit dotplot:

# construct a prediction grid for the fit line
prediction_grid = with(iris_v,
  data.frame(Petal.Length = seq(min(Petal.Length), max(Petal.Length), length.out = 100))
)

prediction_grid %>%
  bind_cols(predict(m, ., se.fit = TRUE)) %>%
  mutate(
    # distribution describing uncertainty in log odds
    log_odds = dist_normal(fit, se.fit),
    # inverse-logit transform the log odds to get
    # distribution describing uncertainty in Pr(Species == "virginica")
    p_virginica = dist_transformed(log_odds, plogis, qlogis)
  ) %>%
  ggplot(aes(x = Petal.Length)) +
  geom_dots(
    aes(y = as.numeric(Species == "virginica"), side = Species),
    scale = 0.4,
    data = iris_v
  ) +
  stat_lineribbon(
    aes(ydist = p_virginica), alpha = 1/4, fill = "#08306b"
  ) +
  scale_side_mirrored(guide = "none") +
  coord_cartesian(ylim = c(0, 1)) +
  labs(
    title = "logit dotplot: geom_dots() with stat_lineribbon()",
    subtitle = 'aes(side = Species) + scale_side_mirrored()',
    x = "Petal Length",
    y = "Pr(Species = virginica)"
  )

Matthew Kay

2024-03-04

Introduction

Setup

Anatomy of `geom_dotsinterval()`

Controlling dot layout

Side

Layout

Beeswarm plots

Varying `color`, `fill`, `shape`, and `linewidth`

Varying discrete aesthetics within dot groups

Varying continuous aesthetics within dot groups

Constraining dot size

On discrete distributions

On analytical distributions

Varying continuous aesthetics with analytical distributions

Thresholds

Rain cloud plots

Dotplots with Monte Carlo Standard Error

Logit dotplots

Dots + interval stats and geoms

Matthew Kay

2024-03-04

Introduction

Setup

Anatomy of geom_dotsinterval()

Controlling dot layout

Side

Layout

Beeswarm plots

Varying color, fill, shape, and linewidth

Varying discrete aesthetics within dot groups

Varying continuous aesthetics within dot groups

Constraining dot size

On discrete distributions

On analytical distributions

Varying continuous aesthetics with analytical distributions

Thresholds

Rain cloud plots

Dotplots with Monte Carlo Standard Error

Logit dotplots

Anatomy of `geom_dotsinterval()`

Varying `color`, `fill`, `shape`, and `linewidth`