Frequentist uncertainty visualization

Introduction

This vignette shows how to combine the ggdist geoms with output from the broom package to enable visualization of uncertainty from frequentist models. The general idea is to use xdist and ydist aesthetics supported by ggdist stats to visualize confidence distributions instead of visualizing posterior distributions as we might from a Bayesian model. For more information on the families of geoms and stats in ggdist, see vignette("slabinterval"), vignette("dotsinterval"), and vignette("lineribbon").

Confidence distributions are a way of unifying the notion of sampling distributions, bootstrap distributions, and several other concepts in frequentist inference. They are a convenient tool for visualizing uncertainty in a way that generalizes across Bayesian and frequentist frameworks: where in a Bayesian framework we might visualize a probability distribution, in the frequentist framework we visualize a confidence distribution. This gives us a way to use the same geometries for uncertainty visualization in either framework.

For more on confidence distributions, see: Xie, Min‐ge, and Kesar Singh. Confidence distribution, the frequentist distribution estimator of a parameter: A review. International Statistical Review 81.1 (2013): 3-39.

Setup

The following libraries are required to run this vignette:

library(dplyr)
library(tidyr)
library(ggdist)
library(ggplot2)
library(broom)
library(distributional)

theme_set(theme_ggdist())

Point estimates

We’ll start with an ordinary least squares (OLS) linear regression analysis of this simple dataset:

set.seed(5)
n = 10
n_condition = 5
ABC =
  tibble(
    condition = rep(c("A","B","C","D","E"), n),
    response = rnorm(n * 5, c(0,1,2,1,-1), 0.5)
  )

This is a typical tidy format data frame: one observation per row. Graphically:

ABC %>%
  ggplot(aes(x = response, y = condition)) +
  geom_point(alpha = 0.5) +
  ylab("condition")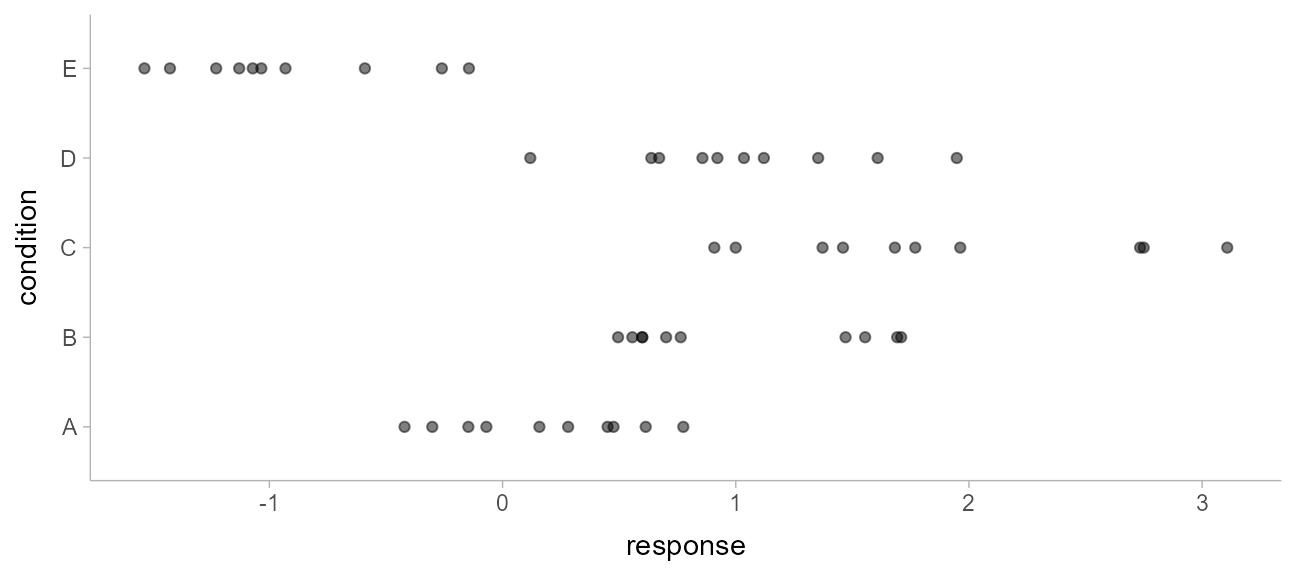

And a simple linear regression of the data is fit as follows:

m_ABC = lm(response ~ condition, data = ABC)

The default summary is not great from an uncertainty communication perspective:

summary(m_ABC)

## 
## Call:
## lm(formula = response ~ condition, data = ABC)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.9666 -0.4084 -0.1053  0.4104  1.2331 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.1816     0.1732   1.048  0.30015    
## conditionB    0.8326     0.2450   3.399  0.00143 ** 
## conditionC    1.6930     0.2450   6.910 1.38e-08 ***
## conditionD    0.8456     0.2450   3.452  0.00122 ** 
## conditionE   -1.1168     0.2450  -4.559 3.94e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5478 on 45 degrees of freedom
## Multiple R-squared:  0.7694, Adjusted R-squared:  0.7489 
## F-statistic: 37.53 on 4 and 45 DF,  p-value: 8.472e-14

So let’s try half-eye plots instead. The basic idea is that we need to get the three parameters for the sampling distribution of each parameter and then use stat_halfeye() to plot them. The confidence distribution for parameter \(i\), \(\tilde\beta_i\), from an lm model is a scaled-and-shifted t distribution:

\[ \tilde\beta_i \sim \textrm{student_t}\left(\nu, \hat\beta_i, \sigma_{\hat\beta_i}\right) \]

With:

\(\nu\): degrees of freedom, equal to df.residual(m_ABC)
\(\hat\beta_i\): location, equal to the point estimate of the parameter (estimate column from broom::tidy())
\(\sigma_{\hat\beta_i}\): scale, equal to the standard error of the parameter estimate (std.error column from broom::tidy())

We can get the estimates and standard errors easily by using broom::tidy():

tidy(m_ABC)

## # A tibble: 5 × 5
##   term        estimate std.error statistic      p.value
##   <chr>          <dbl>     <dbl>     <dbl>        <dbl>
## 1 (Intercept)    0.182     0.173      1.05 0.300       
## 2 conditionB     0.833     0.245      3.40 0.00143     
## 3 conditionC     1.69      0.245      6.91 0.0000000138
## 4 conditionD     0.846     0.245      3.45 0.00122     
## 5 conditionE    -1.12      0.245     -4.56 0.0000394

Finally, we can construct vectors of probability distributions using functions like distributional::dist_student_t() from the distributional package. The stat_slabinterval() family of functions supports these objects.

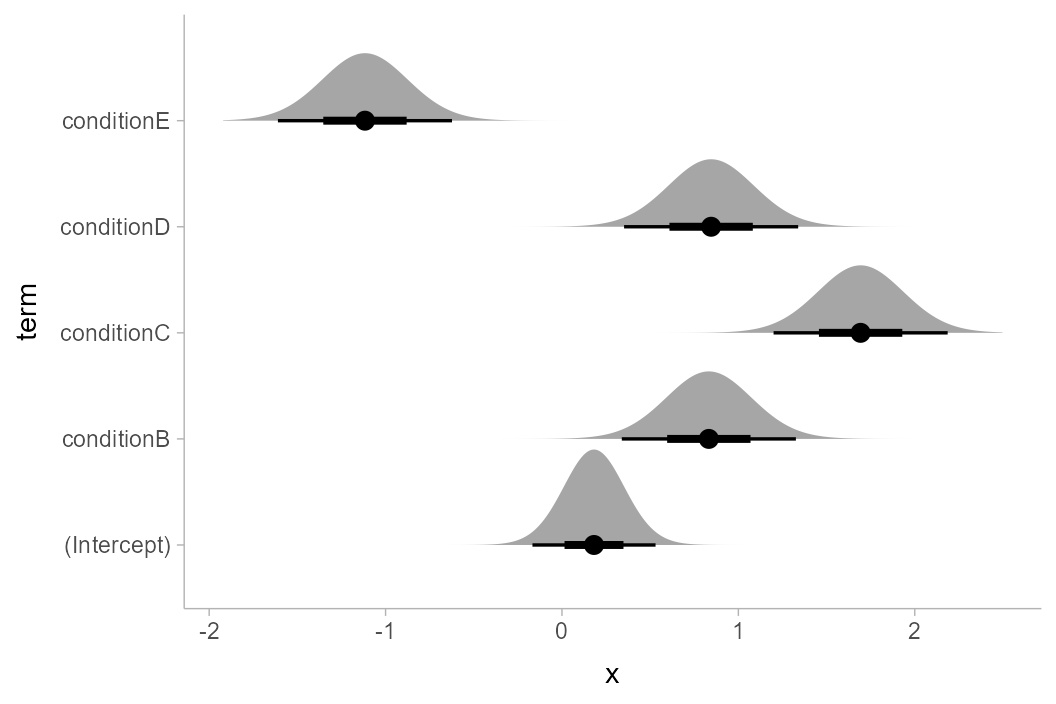
Putting everything together, we have:

m_ABC %>%
  tidy() %>%
  ggplot(aes(y = term)) +
  stat_halfeye(
    aes(xdist = dist_student_t(df = df.residual(m_ABC), mu = estimate, sigma = std.error))
  )

If we would rather see uncertainty in conditional means, we can instead use tidyr::expand() along with broom::augment() (similar to how we can use tidyr::expand() with tidybayes::add_fitted_draws() for Bayesian models). Here we want the confidence distribution for the mean in condition \(c\), \(\tilde\mu_c\):

\[ \tilde\mu_c \sim \textrm{student_t}\left(\nu, \hat\mu_c, \sigma_{\hat\mu_c} \right) \]

With:

\(\nu\): degrees of freedom, equal to df.residual(m_ABC)
\(\hat\mu_c\): location, equal to the point estimate of the mean in condition \(c\) (.fitted column from broom::augment())
\(\sigma_{\hat\mu_c}\): scale, equal to the standard error of the mean in condition \(c\) (.se.fit column from broom::augment(..., se_fit = TRUE))

Putting everything together, we have:

ABC %>%
  expand(condition) %>%
  augment(m_ABC, newdata = ., se_fit = TRUE) %>%
  ggplot(aes(y = condition)) +
  stat_halfeye(
    aes(xdist = dist_student_t(df = df.residual(m_ABC), mu = .fitted, sigma = .se.fit)),
    scale = .5
  ) +
  # we'll add the data back in too (scale = .5 above adjusts the halfeye height so
  # that the data fit in as well)
  geom_point(aes(x = response), data = ABC, pch = "|", size = 2, position = position_nudge(y = -.15))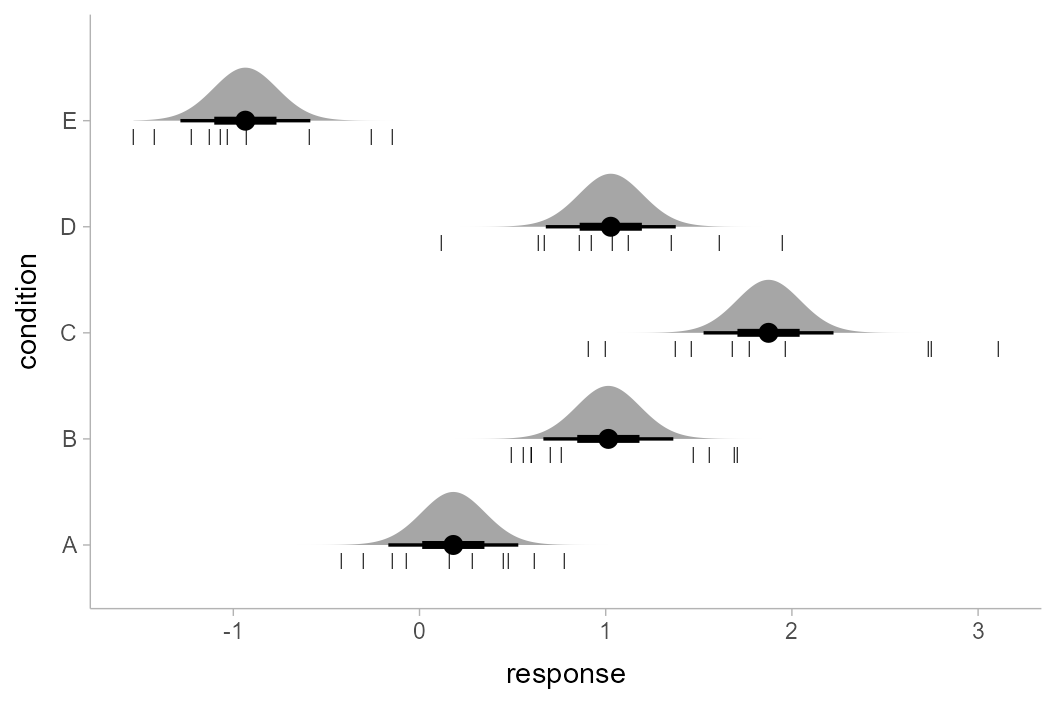

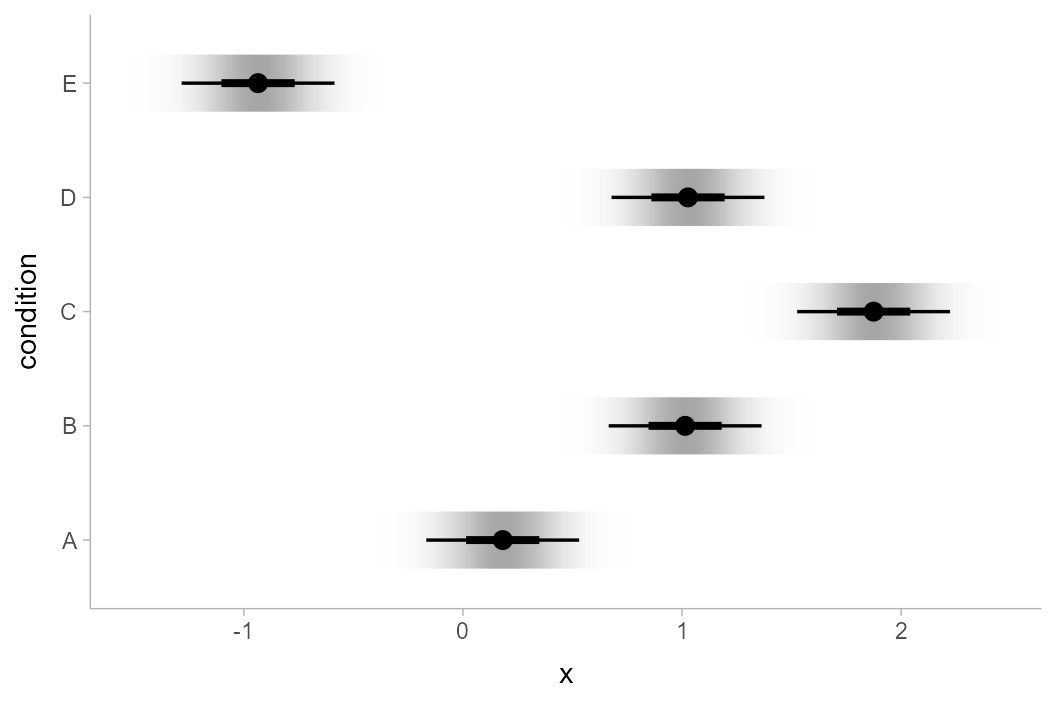
Of course, this works with the entire stat_slabinterval() family. Here are gradient plots instead:

ABC %>%
  expand(condition) %>%
  augment(m_ABC, newdata = ., se_fit = TRUE) %>%
  ggplot(aes(y = condition)) +
  stat_gradientinterval(
    aes(xdist = dist_student_t(df = df.residual(m_ABC), mu = .fitted, sigma = .se.fit)),
    scale = .5, fill_type = "gradient"
  )

Note: The example above uses the experimental fill_type = "gradient" option. This can be omitted if your system does not support it; see further discussion in the section on gradient plots in vignette("slabinterval").

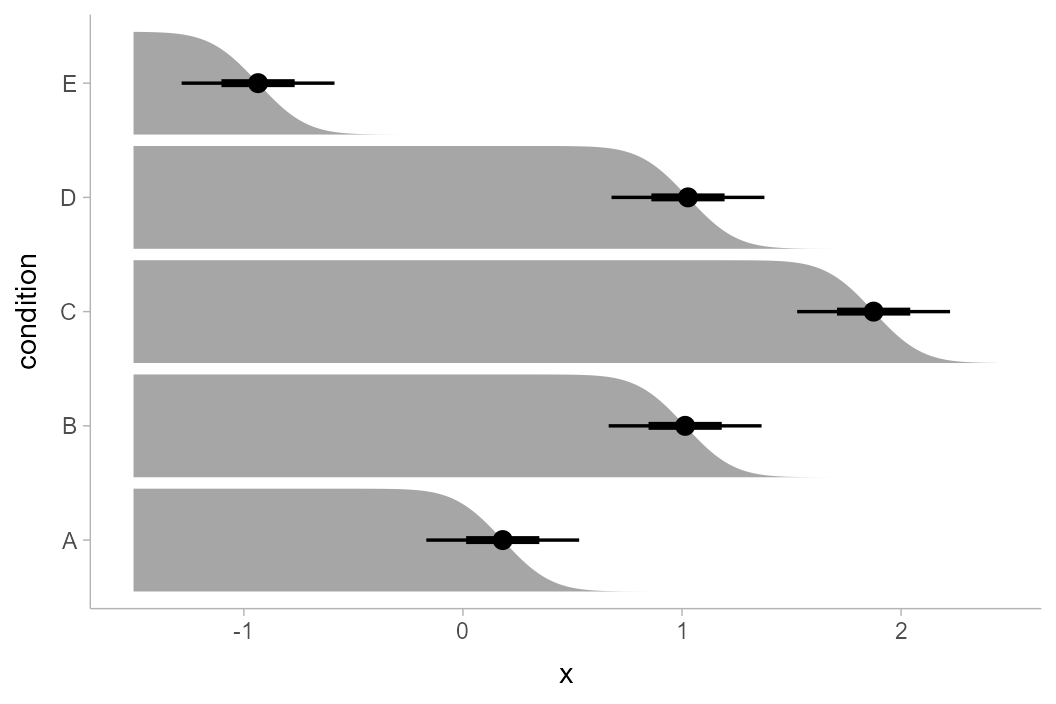
Or complementary cumulative distribution function (CCDF) bar plots:

ABC %>%
  expand(condition) %>%
  augment(m_ABC, newdata = ., se_fit = TRUE) %>%
  ggplot(aes(y = condition)) +
  stat_ccdfinterval(
    aes(xdist = dist_student_t(df = df.residual(m_ABC), mu = .fitted, sigma = .se.fit))
  )

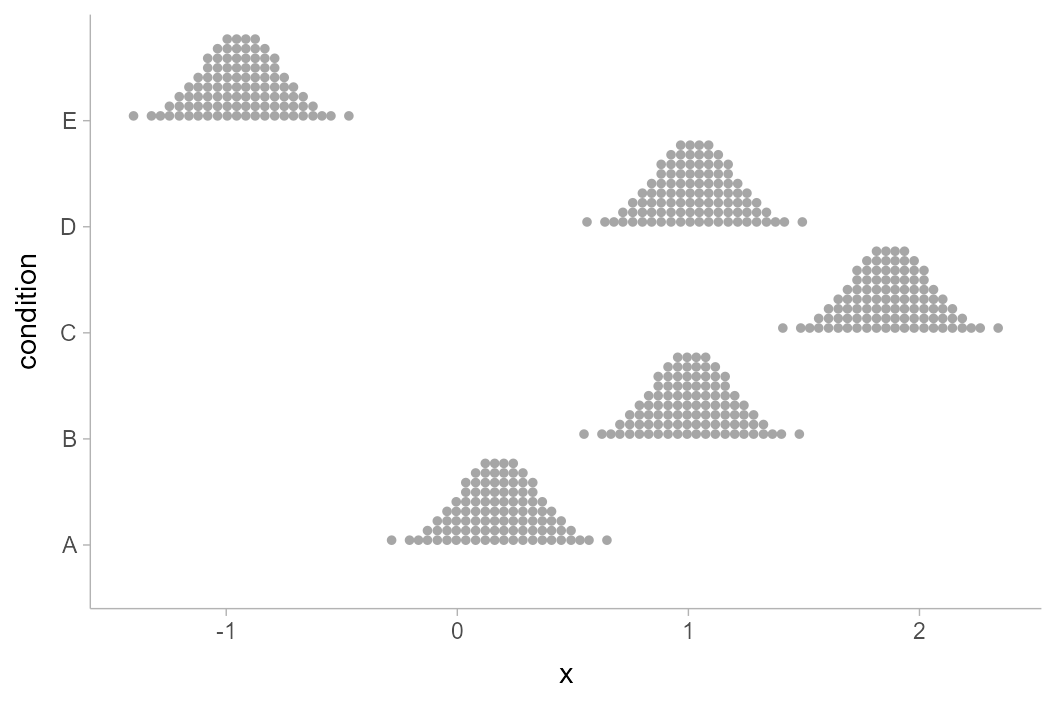
We can also create quantile dotplots by using the dots family of geoms. Quantile dotplots show quantiles from a distribution (in this case, the sampling distribution), employing a frequency framing approach to uncertainty communication that can be easier for people to interpret (Kay et al. 2016, Fernandes et al. 2018):

ABC %>%
  expand(condition) %>%
  augment(m_ABC, newdata = ., se_fit = TRUE) %>%
  ggplot(aes(y = condition)) +
  stat_dots(
    aes(xdist = dist_student_t(df = df.residual(m_ABC), mu = .fitted, sigma = .se.fit)),
    quantiles = 100
  )

See vignette("slabinterval") and vignette("dotsinterval") for more examples of uncertainty geoms and stats in the slabinterval family.

For a fit line

The same principle of reconstructing the confidence distribution allows us to use stat_lineribbon() to construct uncertainty bands around regression fit lines. Here we’ll reconstruct an example with the mtcars dataset from vignette("tidy-brms", package = "tidybayes"), but using lm() instead:

m_mpg = lm(mpg ~ hp * cyl, data = mtcars)

Again we’ll use tidyr::expand() with broom::tidy(), but now we’ll employ stat_lineribbon():

mtcars %>%
  group_by(cyl) %>%
  expand(hp = seq(min(hp), max(hp), length.out = 101)) %>%
  augment(m_mpg, newdata = ., se_fit = TRUE) %>%
  ggplot(aes(x = hp, fill = ordered(cyl), color = ordered(cyl))) +
  stat_lineribbon(
    aes(ydist = dist_student_t(df = df.residual(m_mpg), mu = .fitted, sigma = .se.fit)),
    alpha = 1/4
  ) +
  geom_point(aes(y = mpg), data = mtcars) +
  scale_fill_brewer(palette = "Set2") +
  scale_color_brewer(palette = "Dark2") +
  labs(
    color = "cyl",
    fill = "cyl",
    y = "mpg"
  )

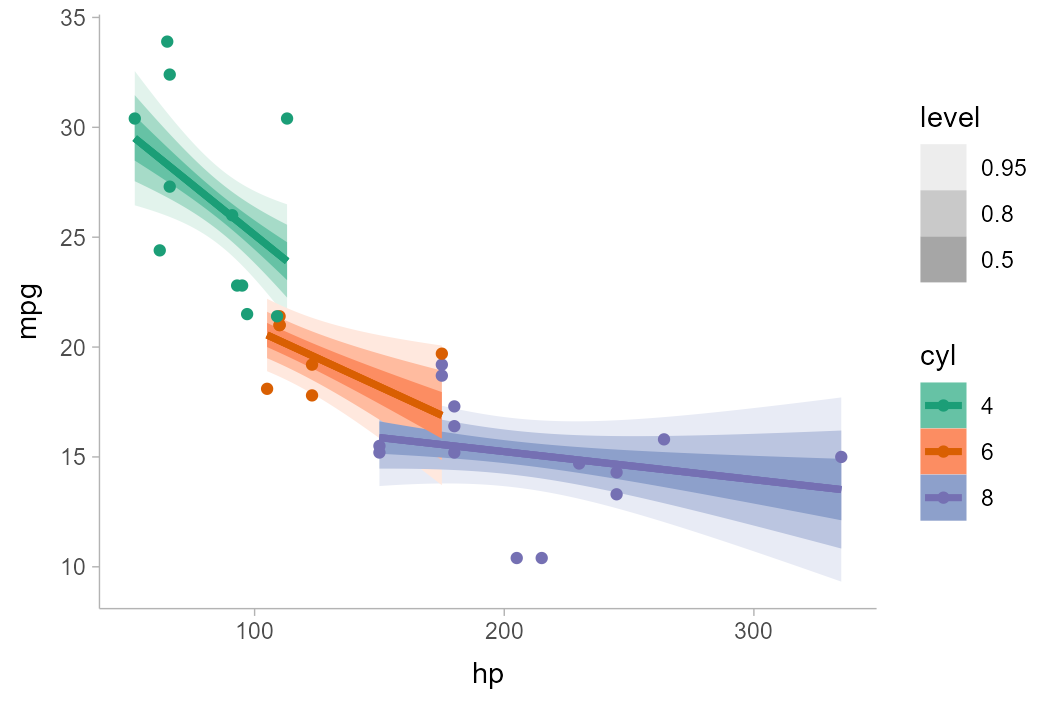
Another alternative to using alpha to create gradations of lineribbon colors in different groups is to use the fill_ramp aesthetic provided by ggdist to “ramp” the fill color of the ribbons from "white" to their full color (see help("scale_fill_ramp")). Here we’ll “whiten” the fill color of each band according to its level (the level variable is computed by stat_lineribbon() and is an ordered factor version of .width):

mtcars %>%
  group_by(cyl) %>%
  expand(hp = seq(min(hp), max(hp), length.out = 101)) %>%
  augment(m_mpg, newdata = ., se_fit = TRUE) %>%
  ggplot(aes(x = hp, color = ordered(cyl))) +
  stat_lineribbon(aes(
    ydist = dist_student_t(df = df.residual(m_mpg), mu = .fitted, sigma = .se.fit),
    fill = ordered(cyl),
    fill_ramp = after_stat(level)
  )) +
  geom_point(aes(y = mpg), data = mtcars) +
  scale_fill_brewer(palette = "Set2") +
  scale_color_brewer(palette = "Dark2") +
  labs(
    color = "cyl",
    fill = "cyl",
    y = "mpg"
  )

One way to avoid problems created by overlapping ribbons (besides using alpha, as above) is to use commutative blending modes available in R > 4.2. The ggblend package enables support for such blending modes, and its documentation includes examples of their use with stat_lineribbon().

For more examples of using lineribbons, see vignette("lineribbon").

Matthew Kay

2024-03-03

Introduction

Setup

Point estimates

For a fit line