Lineribbon stats and geoms

Introduction

The following vignette describes the geom_lineribbon() family of stats and geoms in ggdist, a family of stats and geoms for creating line+ribbon plots: for example, plots with a fit line and one or more uncertainty bands. This vignette also describes the curve_interval() function for calculating curvewise (joint) intervals for lineribbon plots.

Setup

The following libraries are required to run this vignette:

library(dplyr)
library(tidyr)
library(ggdist)
library(ggplot2)
library(distributional)
library(patchwork)

theme_set(theme_ggdist())

The lineribbon family

The lineribbon family follows the same naming scheme as the larger family of slabinterval geoms (see vignette("slabinterval")). It has two members: geom_lineribbon() and stat_lineribbon().

geom_lineribbon() can be used on data already summarized into points and intervals.
stat_lineribbon() can be used:
- on sample data by mapping values onto the x or y aesthetic. For example, it could be used with draws from a posterior distribution of lines/curves, a bootstrap sampling distribution of lines/curves, an ensemble distribution, or any other distribution, really. This stat computes relevant summaries (points and intervals) before forwarding the summaries to geom_lineribbon().
- on analytical distributions by mapping distributions onto the xdist or ydist aesthetic. It takes distributional objects, posterior::rvar() objects, or distribution names (the dist aesthetic) and arguments (the args aesthetic or arg1, … arg9 aesthetics) and computes the relevant slabs and intervals.

All lineribbon geoms can be plotted horizontally or vertically. Depending on how aesthetics are mapped, they will attempt to automatically determine the orientation; if this does not produce the correct result, the orientation can be overridden by setting orientation = "horizontal" or orientation = "vertical".

Lineribbons on already-summarized data

The base lineribbon geometry can only be applied to already-summarized data: data frames where each row contains a point and the upper and lower bounds of an interval. For the purposes of this example, we will first look at how to generate such a data frame from a data frame of sample data; such data could include Bayesian posterior distributions (for examples of this usage, see vignettes in tidybayes) or bootstrap sampling distributions. For the simple example here, we’ll just generate a distribution of lines manually:

set.seed(1234)
n = 5000

df = tibble(
  .draw = 1:n,
  intercept = rnorm(n, 3, 1),
  slope = rnorm(n, 1, 0.25),
  x = list(-4:5),
  y = Map(function(x, y) x + y * -4:5, intercept, slope)
) %>%
  unnest(c(x, y))

df is a 50,000-row data frame with a sample of 5000 y values for each x value. It represents a sample of 5000 lines. Here is a subsample of 100 of the lines:

df %>%
  filter(.draw %in% 1:100) %>%
  ggplot(aes(x = x, y = y, group = .draw)) +
  geom_line(alpha = 0.25)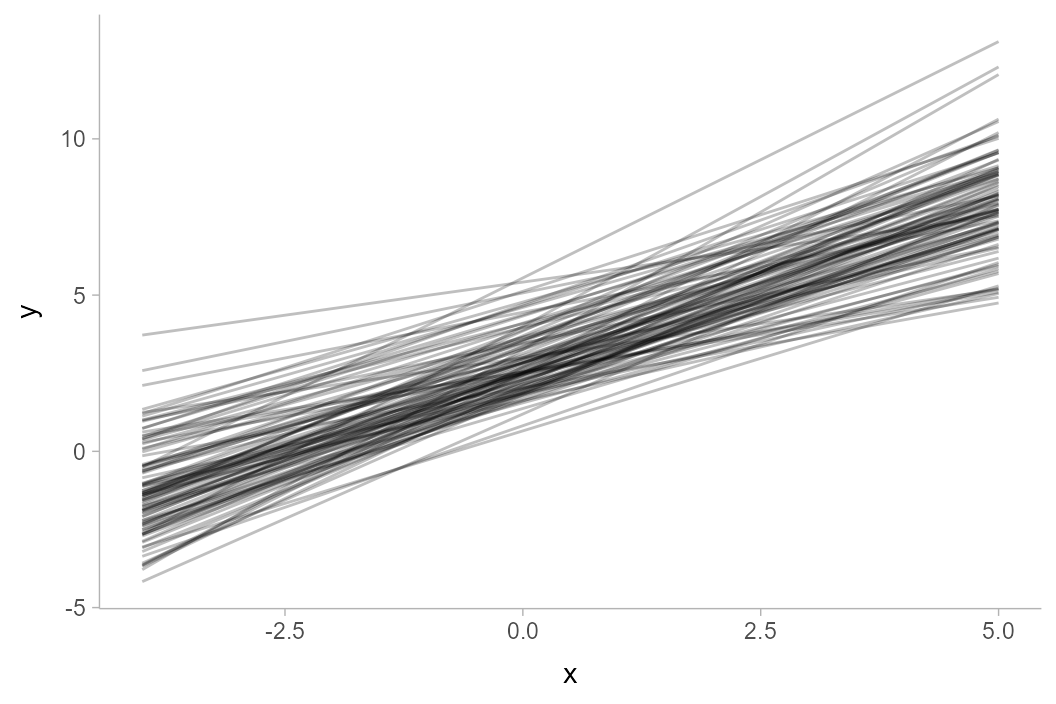

We can summarize the data frame at each x position using median_qi() (or any other function in the point_interval() family):

df %>%
  group_by(x) %>%
  median_qi(y)

## # A tibble: 10 × 7
##        x       y    .lower .upper .width .point .interval
##    <int>   <dbl>     <dbl>  <dbl>  <dbl> <chr>  <chr>    
##  1    -4 -1.01   -3.71       1.61   0.95 median qi       
##  2    -3 -0.0149 -2.38       2.30   0.95 median qi       
##  3    -2  0.981  -1.14       3.07   0.95 median qi       
##  4    -1  2.00    0.000809   3.97   0.95 median qi       
##  5     0  2.99    1.07       4.94   0.95 median qi       
##  6     1  3.99    2.04       6.00   0.95 median qi       
##  7     2  4.99    2.88       7.14   0.95 median qi       
##  8     3  6.00    3.58       8.44   0.95 median qi       
##  9     4  7.00    4.25       9.81   0.95 median qi       
## 10     5  8.01    4.89      11.2    0.95 median qi

Given data summarized like that above, we can then construct a line+ribbon chart using geom_lineribbon():

df %>%
  group_by(x) %>%
  median_qi(y) %>%
  ggplot(aes(x = x, y = y, ymin = .lower, ymax = .upper)) +
  geom_lineribbon(fill = "gray65")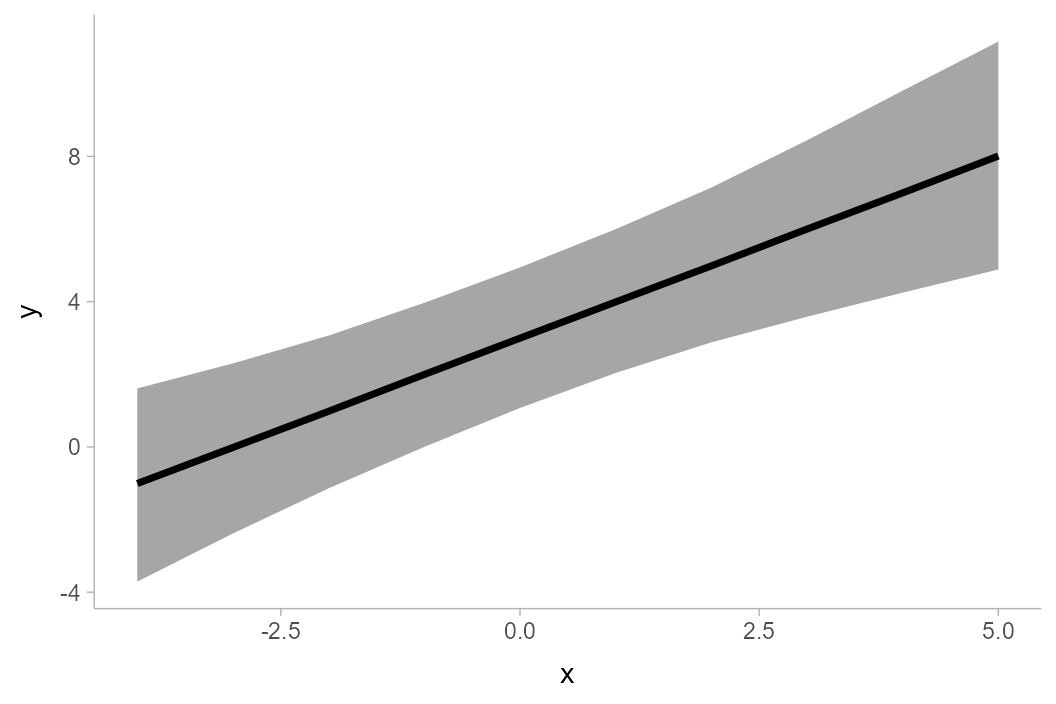

geom_lineribbon() automatically pulls in the .width column and maps it onto the fill aesthetic so that intervals of different widths get different colors. However, the result with just one interval is not great, as the default color scheme is quite dark with just one color. Let’s make two changes to improve the chart:

We will use the .width argument of median_qi() to generate multiple uncertainty bands (a 50%, 80%, and 95% band).
We will use scale_fill_brewer() to get a nicer color scheme.

The result looks like this:

df %>%
  group_by(x) %>%
  median_qi(y, .width = c(.50, .80, .95)) %>%
  ggplot(aes(x = x, y = y, ymin = .lower, ymax = .upper)) +
  geom_lineribbon() +
  scale_fill_brewer()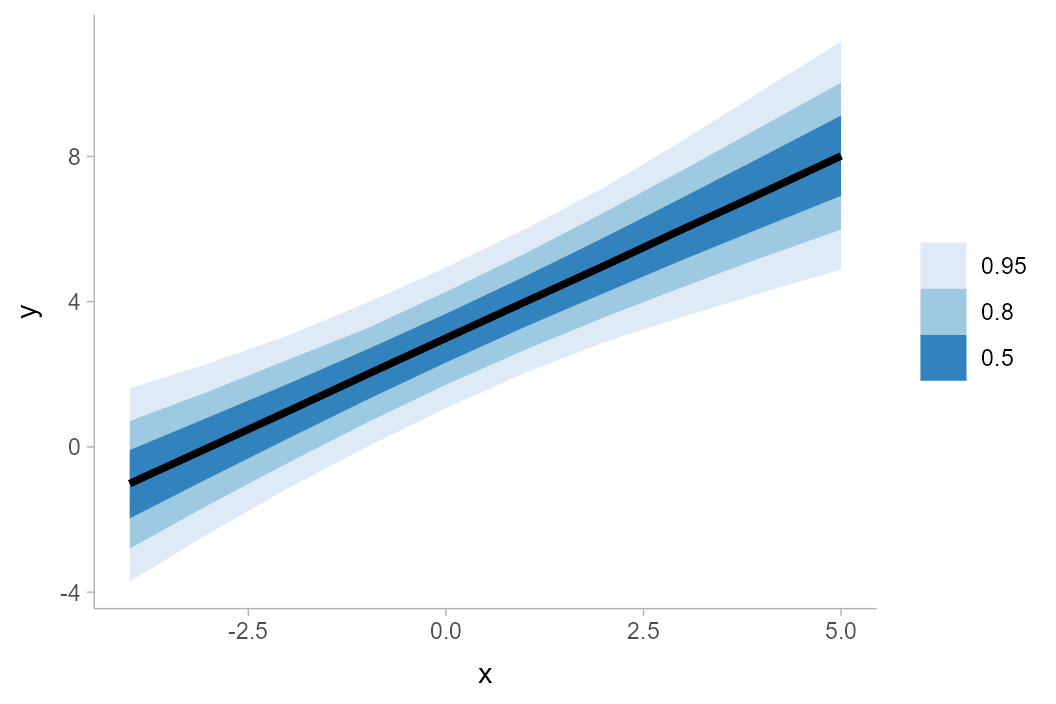

Lineribbons on sample data

To apply lineribbons to sample data, we can also use stat_lineribbon() instead of summarizing the data first using median_qi() or point_interval(). This function does the summarization internally for you.

Taking the previous example, we can simply removing the lines that summarize the data first, and omit the aesthetic mappings onto ymin and ymax, which are automatically set by stat_lineribbon(). This simplifies the previous example considerably:

df %>%
  ggplot(aes(x = x, y = y)) +
  stat_lineribbon() +
  scale_fill_brewer()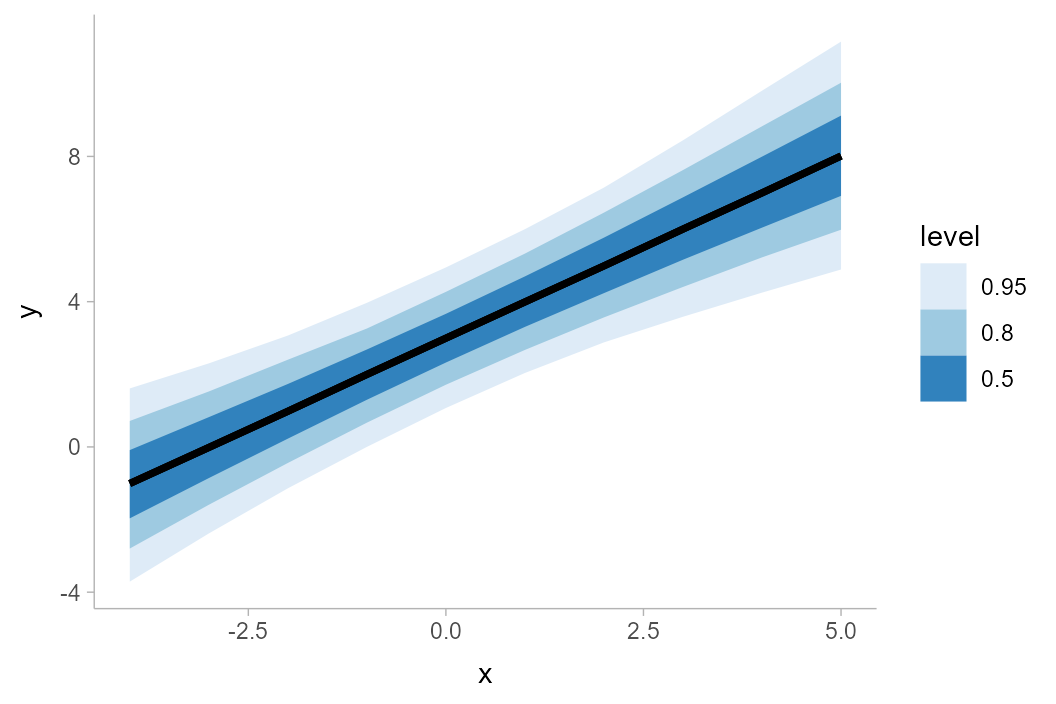

The default .width setting of stat_lineribbon() is c(.50, .80, .95), as can be seen in the results above. We can change this to get other sets of any number of intervals (e.g., c(.66, .95), c(.80, .95, .99), etc).

Lineribbon “gradients”

You can also create gradient-like plots with lineribbons by passing a large number of probability levels to the .width parameter. Calling ppoints(n) generates n values between 0 and 1 (exclusive), which can be used as interval widths. We must also override the default fill aesthetic to use the .width generated variable, which is continuous (by default lineribbons map level onto the fill aesthetic, which is a transformation of .width into a factor—and produces illegible legends when many values are used). This also requires us to use a continuous fill scale (e.g. scale_fill_distiller()) instead of a discrete one (e.g. scale_fill_brewer()):

df %>%
  ggplot(aes(x = x, y = y, fill = after_stat(.width))) +
  stat_lineribbon(.width = ppoints(50)) +
  scale_fill_distiller() +
  labs(title = "stat_lineribbon(.width = ppoints(50))")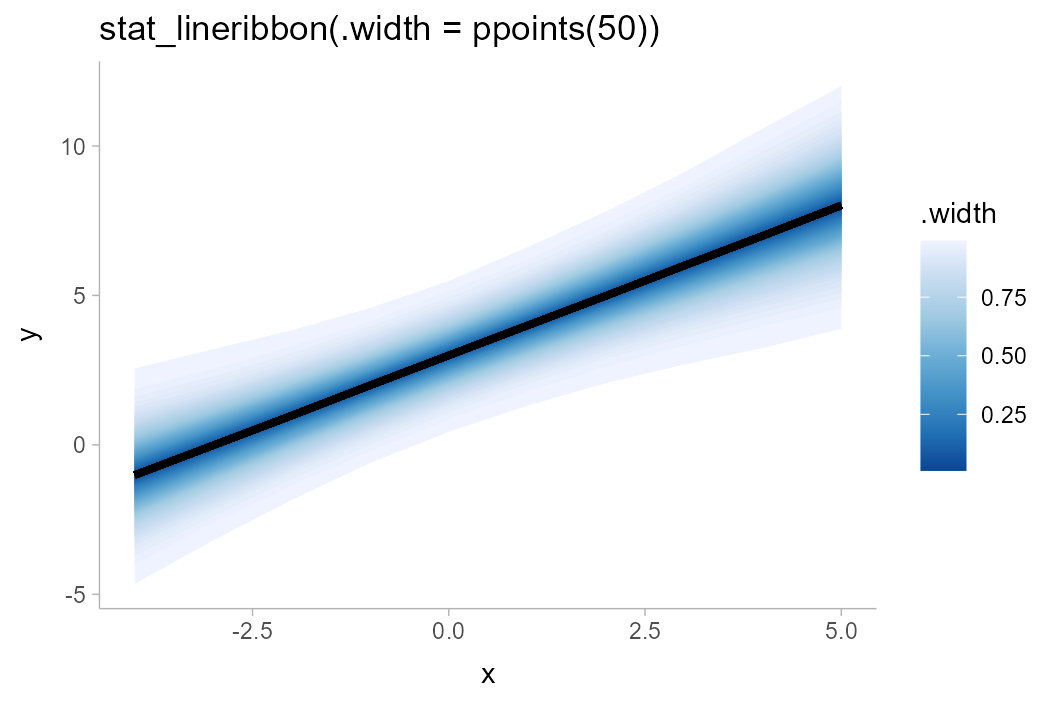

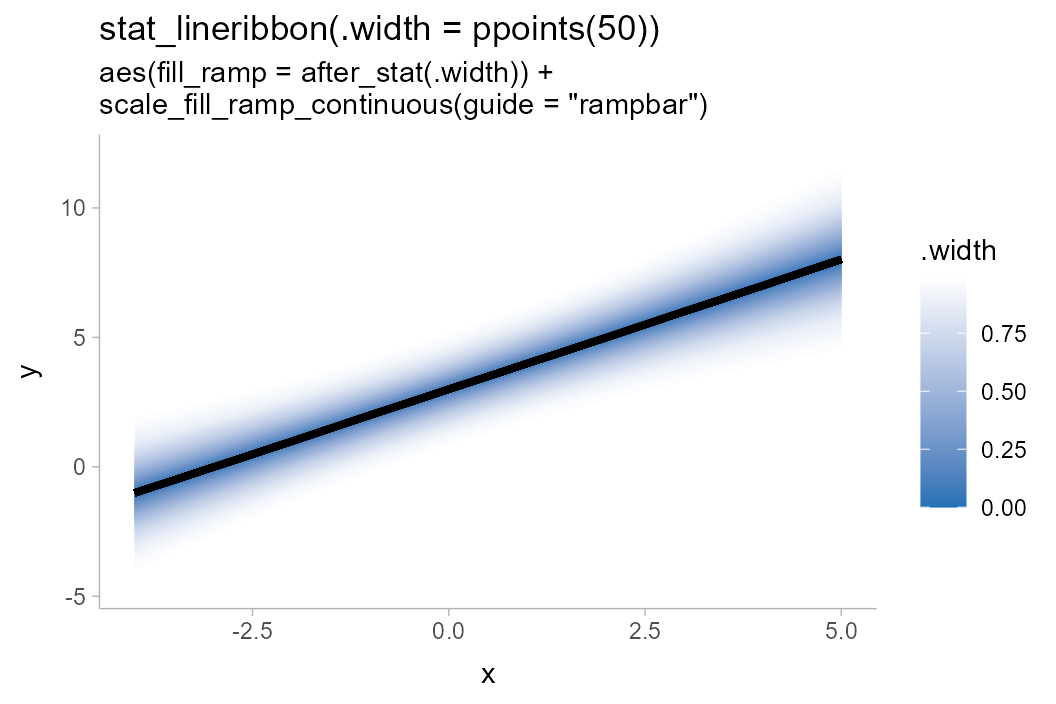
To get a gradient that ramps down to the background color, you could also use the fill_ramp aesthetic provided by ggdist (see help("scale_fill_ramp")). It is necessary to invert the range (range = c(1, 0)) so that the gradient is dark in the middle (rather than the outside).

The default legend for the fill_ramp and color_ramp scales is guide_legend(), which uses discrete legends even for continuous scales. To get a gradient-style legend, use guide_rampbar(), and if necessary, use the to = argument to specify the color to ramp to in the legend (default is "gray65"):

df %>%
  ggplot(aes(x = x, y = y, fill_ramp = after_stat(.width))) +
  stat_lineribbon(.width = ppoints(50), fill = "#2171b5") +
  scale_fill_ramp_continuous(range = c(1, 0), guide = guide_rampbar(to = "#2171b5")) +
  labs(
    title = "stat_lineribbon(.width = ppoints(50))",
    subtitle = 'aes(fill_ramp = after_stat(.width)) +\nscale_fill_ramp_continuous(guide = "rampbar")'
  )

It’s worth noting that the use of .width as the fill color means these gradients are akin to classical “fan” charts; i.e. the fill color is proportional to the folded CDF or the so-called “confidence function”. We may instead want the fill color to be proportional to the density.

Lineribbon density gradients

Making the fill proportional to density is a bit more complicated to achieve, but can be approximated using an experimental feature in the latest version of ggdist. This feature exposes density and CDF information to interval sub-geometries. As this feature is fragile and not fully supported across all scenarios of use, it must be enabled by setting options(ggdist.experimental.slab_data_in_intervals = TRUE).

Internally, with this feature enabled, ggdist calculates the density of the lower (pdf_min) and upper (pdf_max) ends of the intervals; you can use the average of these (or just their sum, since we don’t need to care about normalizing constants) as an approximation of the density for each interval. These averages must be taken within values of .width so that each strip gets the same fill color, which can be done using the ave() function, which takes the average of its first argument within groups of the second:

withr::with_options(list(ggdist.experimental.slab_data_in_intervals = TRUE), print(
  df %>%
    ggplot(aes(x = x, y = y, fill_ramp = after_stat(ave(pdf_min + pdf_max, .width)))) +
    stat_lineribbon(.width = ppoints(50), fill = "#2171b5") +
    scale_fill_ramp_continuous(name = "density", guide = guide_rampbar(to = "#2171b5")) +
    labs(
      title = "stat_lineribbon(.width = ppoints(50))",
      subtitle = 'aes(fill_ramp = after_stat(ave(pdf_min + pdf_max, .width)))'
    )
))

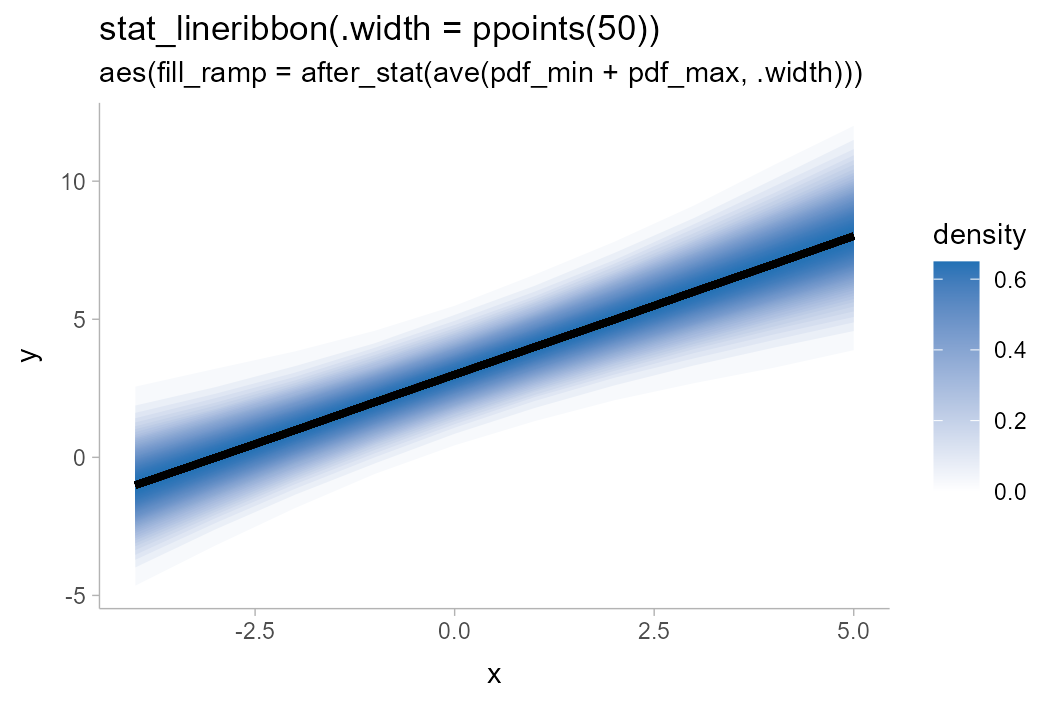
You may notice that the steps in the gradient now look a little “jumpy” near the edges of the band: this is because the ppoints() function is giving us even steps in probability space (i.e. the CDF), which are not even steps in terms of density. It is not strictly necessary to fix for the correctness of the color, but is more visually appealing without the jumpiness.

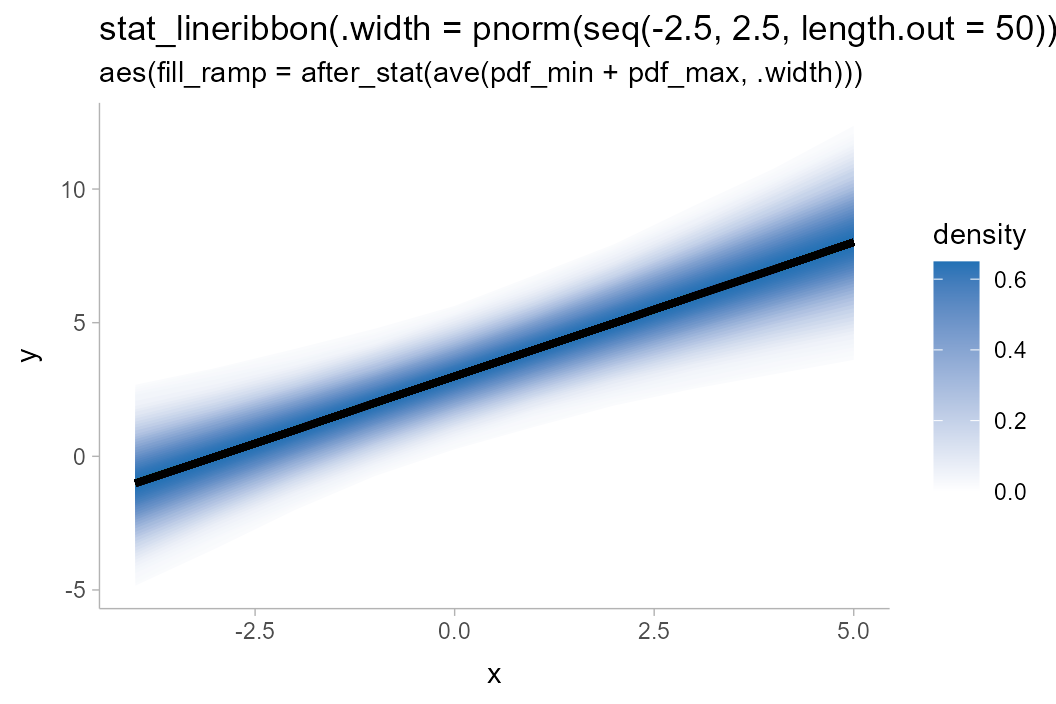
We can pick some steps that are more likely to be even in density space using evenly-spaced z values and translating them into probability levels using pnorm(). It does not matter if our target distribution is non-Normal, since the actual densities are still set using pdf_min and pdf_max (so colors will still be correct), but the closer the distribution is to Normal the less jumpy-looking the gradient will be.

withr::with_options(list(ggdist.experimental.slab_data_in_intervals = TRUE), print(
  df %>%
    ggplot(aes(x = x, y = y, fill_ramp = after_stat(ave(pdf_min + pdf_max, .width)))) +
    stat_lineribbon(.width = pnorm(seq(-2.5, 2.5, length.out = 50)), fill = "#2171b5") +
    scale_fill_ramp_continuous(name = "density", guide = guide_rampbar(to = "#2171b5")) +
    labs(
      title = "stat_lineribbon(.width = pnorm(seq(-2.5, 2.5, length.out = 50)))",
      subtitle = 'aes(fill_ramp = after_stat(ave(pdf_min + pdf_max, .width)))'
    )
))

If you are using a different background color than "white", you can pass that color to the from argument of scale_fill_ramp_continuous() to ramp from that color to the fill color of the lineribbon.

Multiple lineribbons on one plot

One may also want to plot multiple lineribbons on the same plot, perhaps corresponding to separate groups. This might require applying a different color or fill to differentiate the lineribbons. Consider these data:

df_2groups = rbind(
  mutate(df, g = "a"),
  mutate(df, g = "b", y = (y - 2) * 0.5)
)

The naive approach to plotting will make the lines hard to distinguish:

df_2groups %>%
  ggplot(aes(x = x, y = y, color = g)) +
  stat_lineribbon() +
  scale_fill_brewer()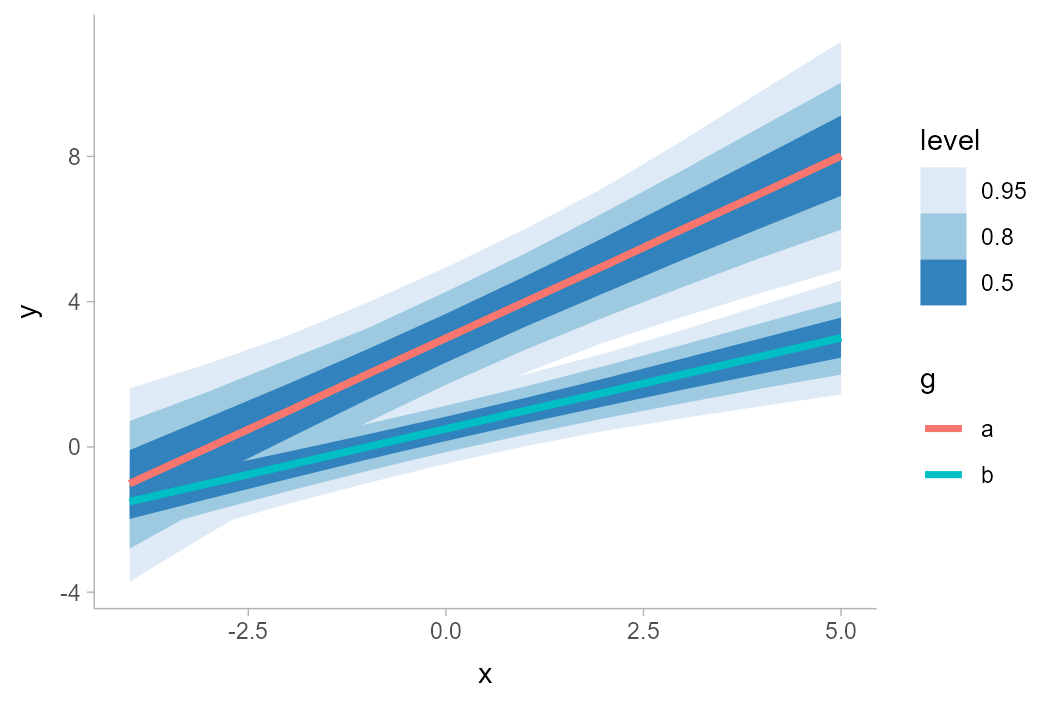

Instead, we could change the fill color and allow the lines the be semi-transparent:

df_2groups %>%
  ggplot(aes(x = x, y = y, fill = g)) +
  stat_lineribbon(alpha = 1/4) +
  labs(title = "stat_lineribbon(aes(fill = g), alpha = 1/4)")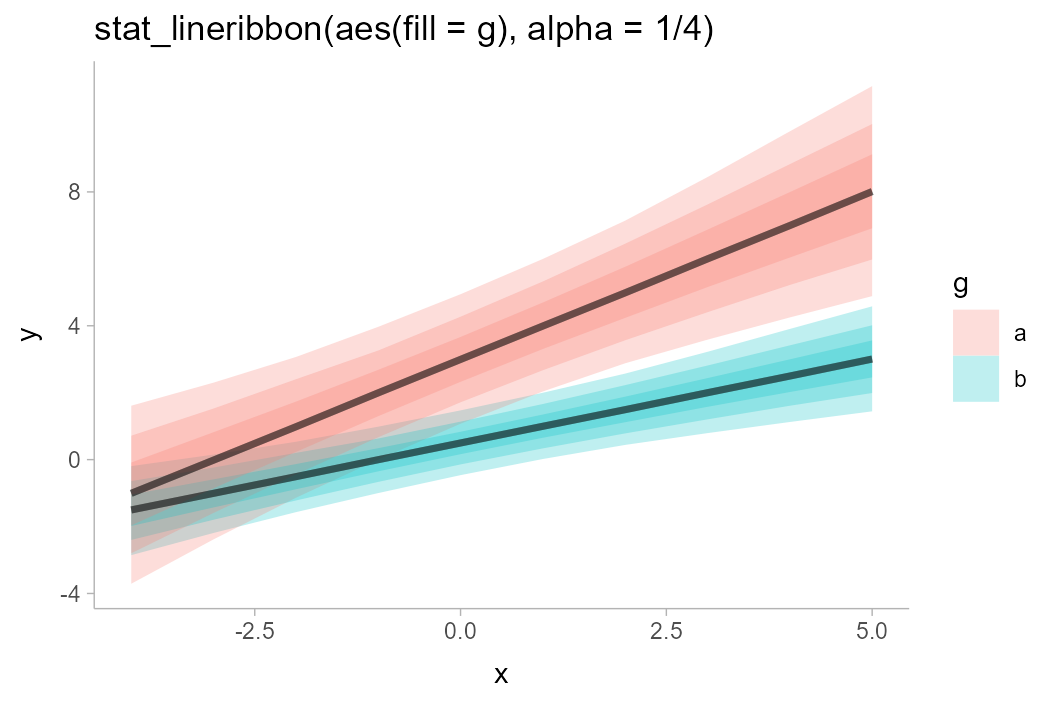

We could also use the fill_ramp aesthetic provided by ggdist to similar effect (see help("scale_fill_ramp")), though this tends to work best when the lines do not overlap:

df_2groups %>%
  ggplot(aes(x = x, y = y, fill = g)) +
  stat_lineribbon(aes(fill_ramp = after_stat(level))) +
  labs(title = "stat_lineribbon(aes(fill = g, fill_ramp = after_stat(level)))")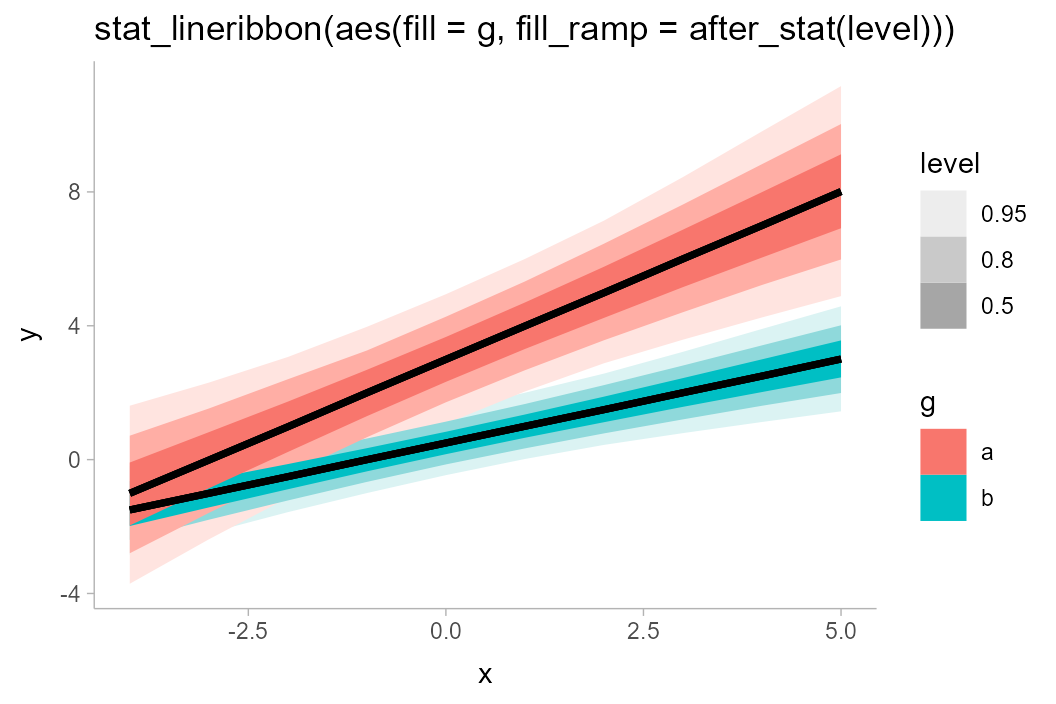

One way to avoid problems created by overlapping ribbons (besides using alpha, as above) is to use commutative blending modes available in R > 4.2. The ggblend package enables support for such blending modes, and its documentation includes examples of their use with stat_lineribbon().

In some situations, you may also try controlling the draw order of ribbons directly, by adjusting the order aesthetic. By default, if the order aesthetic is not specified, geom_lineribbon() draws ribbons that are widest on average at the bottom. stat_lineribbon(), by default, is a bit smarter, and sets the order aesthetic to after_stat(level), using the level computed variable to draw ribbons in order of their confidence / probability mass. An alternative might be to draw all ribbons from the same group on top of each other, like so:

df_2groups %>%
  ggplot(aes(x = x, y = y, fill = g)) +
  stat_lineribbon(aes(
    fill_ramp = after_stat(level),
    order = after_stat(interaction(level, group))
  )) +
  labs(title = "stat_lineribbon(aes(order = after_stat(interaction(level, group))))")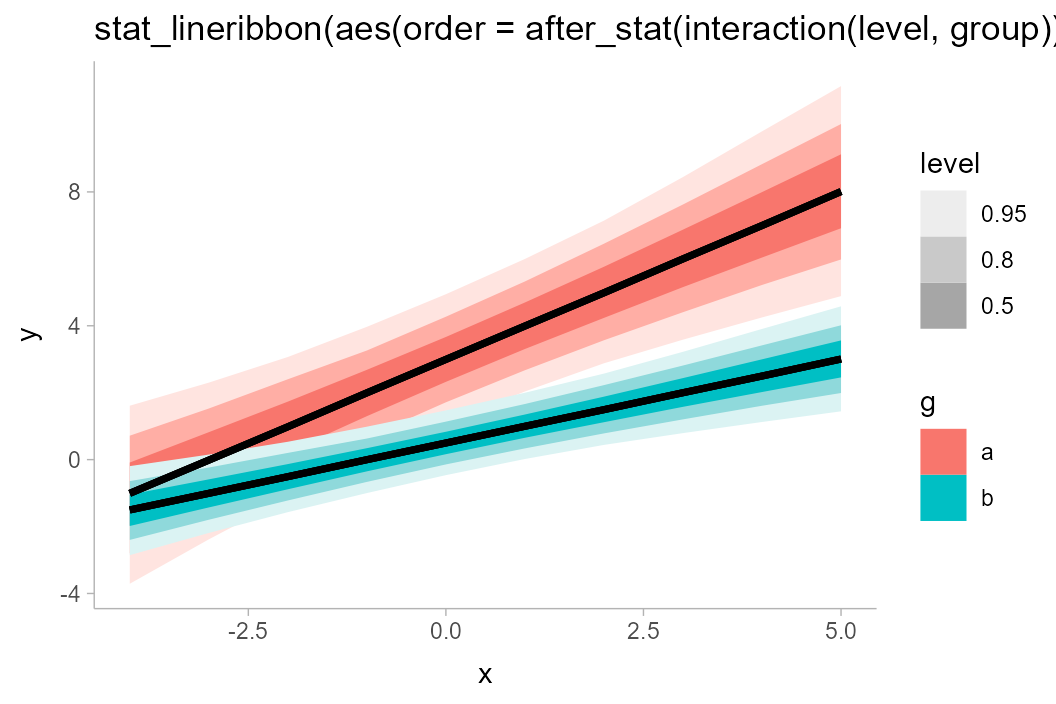

Lineribbons on analytical distributions

Lineribbons can also be applied to analytical distributions. This use case often arises with confidence distributions describing uncertainty in a fit line; for an example, see the end of vignette("freq-uncertainty-vis"). Here, we will look at a simpler example where we construct the distributions manually; here we’ll assume some variable y that is normally distributed conditional on x with mean y_mean and standard deviation y_sd:

analytical_df = tibble(
  x = -4:5,
  y_mean = 3 + x,
  y_sd = sqrt(x^2/10 + 1)
)
analytical_df

## # A tibble: 10 × 3
##        x y_mean  y_sd
##    <int>  <dbl> <dbl>
##  1    -4     -1  1.61
##  2    -3      0  1.38
##  3    -2      1  1.18
##  4    -1      2  1.05
##  5     0      3  1   
##  6     1      4  1.05
##  7     2      5  1.18
##  8     3      6  1.38
##  9     4      7  1.61
## 10     5      8  1.87

We can visualize this conditional distribution using stat_lineribbon() with distributional::dist_normal():

analytical_df %>%
  ggplot(aes(x = x, ydist = dist_normal(y_mean, y_sd))) +
  stat_lineribbon() +
  scale_fill_brewer()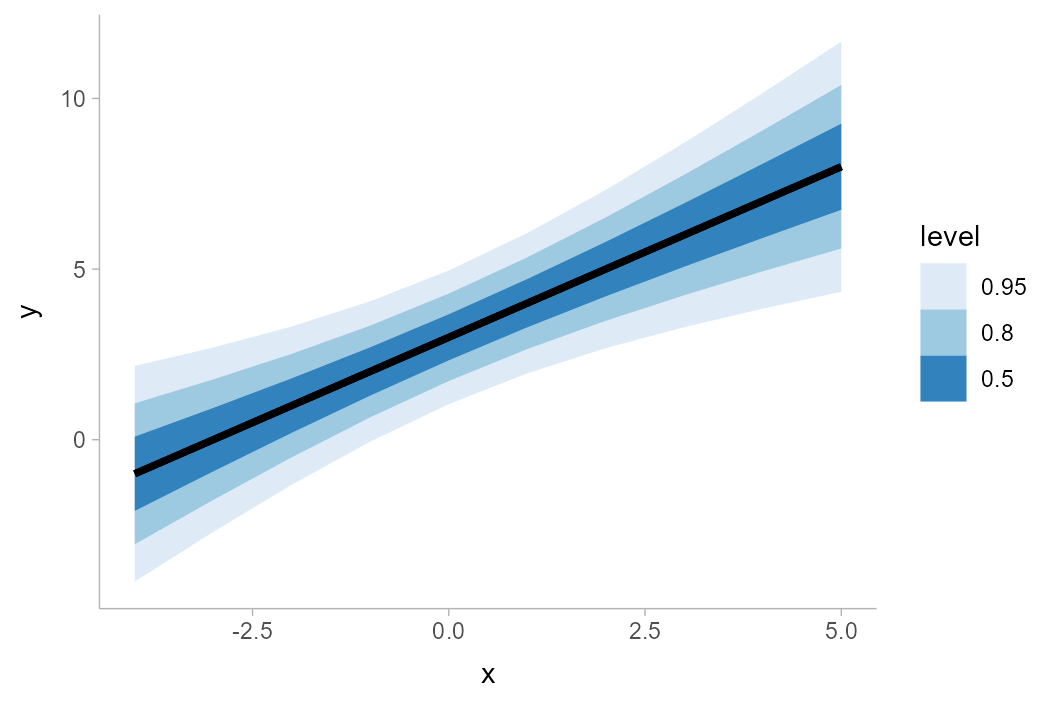

More examples

For more examples of lineribbons, including multiple lineribbons in the same plot, see the examples at the end of vignette("freq-uncertainty-vis").

Curve boxplots (aka lineribbons with joint intervals or curvewise intervals)

The above examples all calculate conditional intervals, either using point_interval() (directly or indirectly) or using quantiles of an analytical distribution. However, you may not always want conditional intervals.

Where point_interval() calculates pointwise intervals, or intervals conditional on each group, curve_interval() calculates joint or curvewise intervals. In the literature these are also called curve boxplots (Mirzargar et al. 2014, Juul et al. 2020).

An example will help illustrate the difference between the two types of intervals. Consider the following set of curves, where each curve is assumed to be a “draw” from some distribution of curves, \(\mathbf{y} = f(\mathbf{x})\), where \(\mathbf{x}\) and \(\mathbf{y}\) are vectors:

k = 11 # number of curves
n = 501
df = tibble(
  .draw = 1:k,
  mean = seq(-5, 5, length.out = k),
  x = list(seq(-15, 15, length.out = n))
) %>%
  unnest(x) %>%
  mutate(y = dnorm(x, mean, 3)/max(dnorm(x, mean, 3)))

df %>%
  ggplot(aes(x = x, y = y)) +
  geom_line(aes(group = .draw), alpha = 0.2)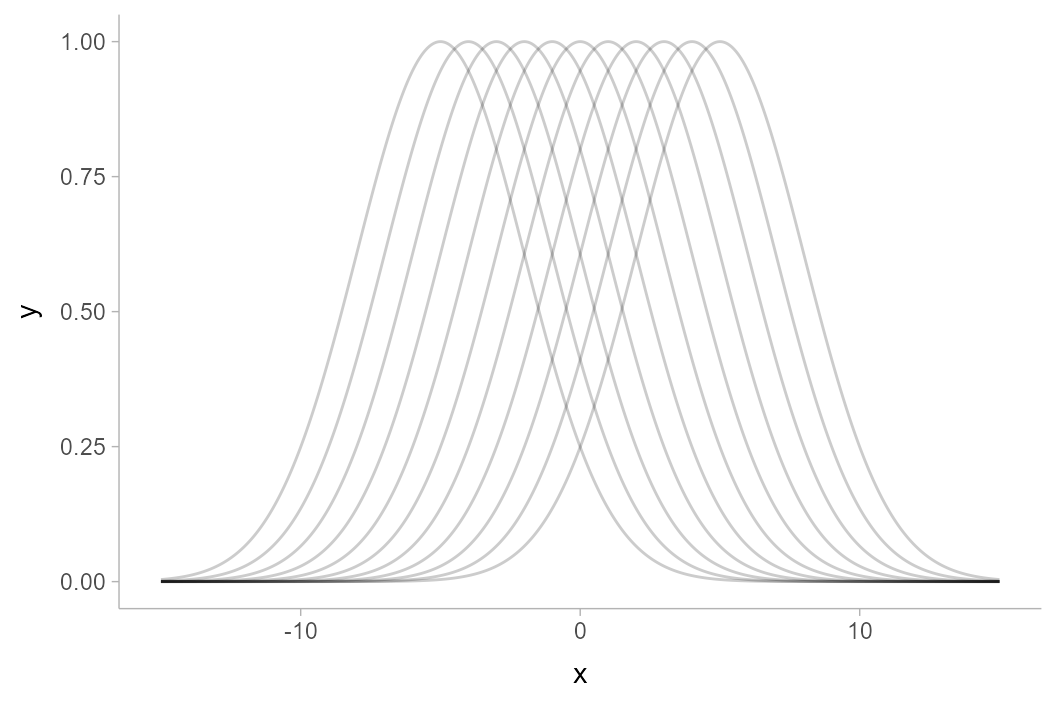

If one used one of the point_interval() functions to summarize this curve (such as median_qi(), mean_qi(), etc), it would calculate pointwise intervals:

df %>%
  group_by(x) %>%
  median_qi(y, .width = .5) %>%
  ggplot(aes(x = x, y = y)) +
  geom_lineribbon(aes(ymin = .lower, ymax = .upper)) +
  geom_line(aes(group = .draw), alpha = 0.15, data = df) +
  scale_fill_brewer() +
  ggtitle("50% pointwise intervals with point_interval()")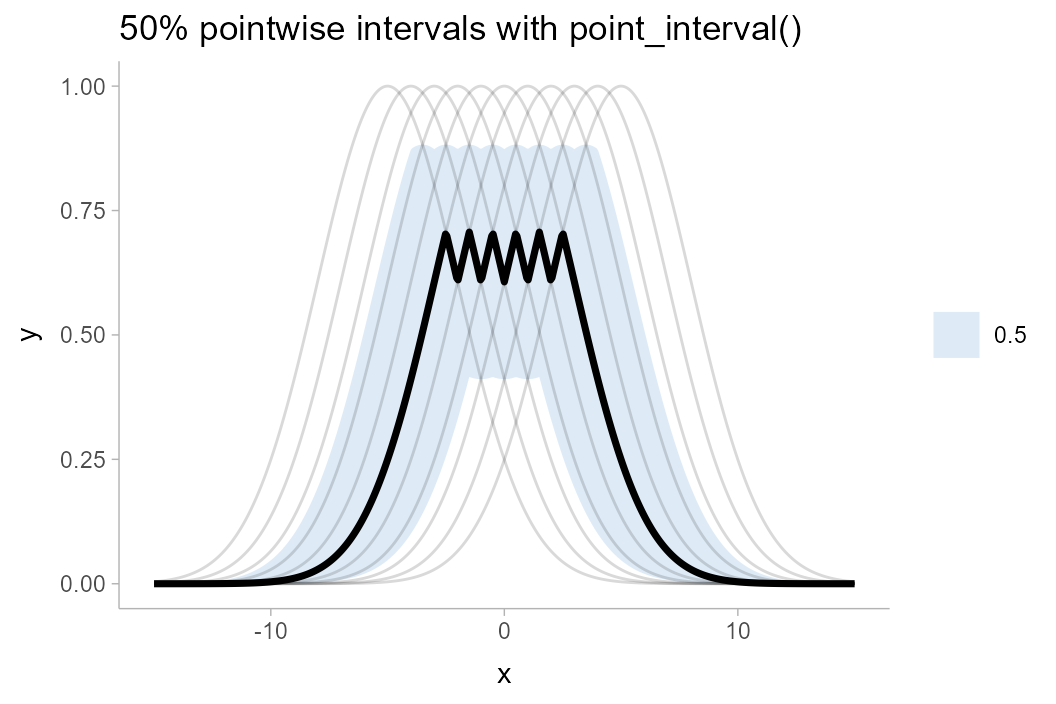

The 50% pointwise interval calculated at (say) \(x = 1\) would contain 50% of the draws from \(y|x=1\). At a different value of \(x\), say \(x = 2\), the 50% pointwise interval would also contain 50% of the draws from \(y|x = 2\). However, the specific draws contained in the interval for \(y|x=2\) might be different draws from those contained in the interval for \(x|y=1\): if you trace any of the underlying curves, you will notice that each curve is included in some intervals and not included in others. Thus, the set of intervals—the ribbon—may not fully contain 50% of curves. Indeed, inspecting the above plot, the 50% ribbon contains none of the curves!

Depending on what type of inference we care about, this might be sufficient for our purposes: maybe we are interested just in what the outcome is likely to be at a given x value (a conditional inference), but we are not interested in joint inferences (e.g., what is the shape of the curve likely to look like?). However, if we are interested in such joint inferences, pointwise intervals can be misleading. The shape of the median curve, for example, looks nothing like any of the possible outcomes. The interval also does not include the maximum value of any of the underlying curves, which might cause us to conclude (incorrectly) that a value close to 1 is unlikely, when the exact opposite is the case (every curve touches 1).

One solution I like for such situations is to show spaghetti plots: just plot the underlying curves. This is a so-called frequency framing uncertainty visualization, and it tends to work fairly well. However, in some cases you may want a visual summary using intervals, in which case curvewise intervals could help. Using curve_interval() instead of point_interval() or median_qi() calculates these:

df %>%
  group_by(x) %>%
  curve_interval(y, .width = .5) %>%
  ggplot(aes(x = x, y = y)) +
  geom_lineribbon(aes(ymin = .lower, ymax = .upper)) +
  geom_line(aes(group = .draw), alpha = 0.15, data = df) +
  scale_fill_brewer() +
  ggtitle("50% curvewise intervals with curve_interval()")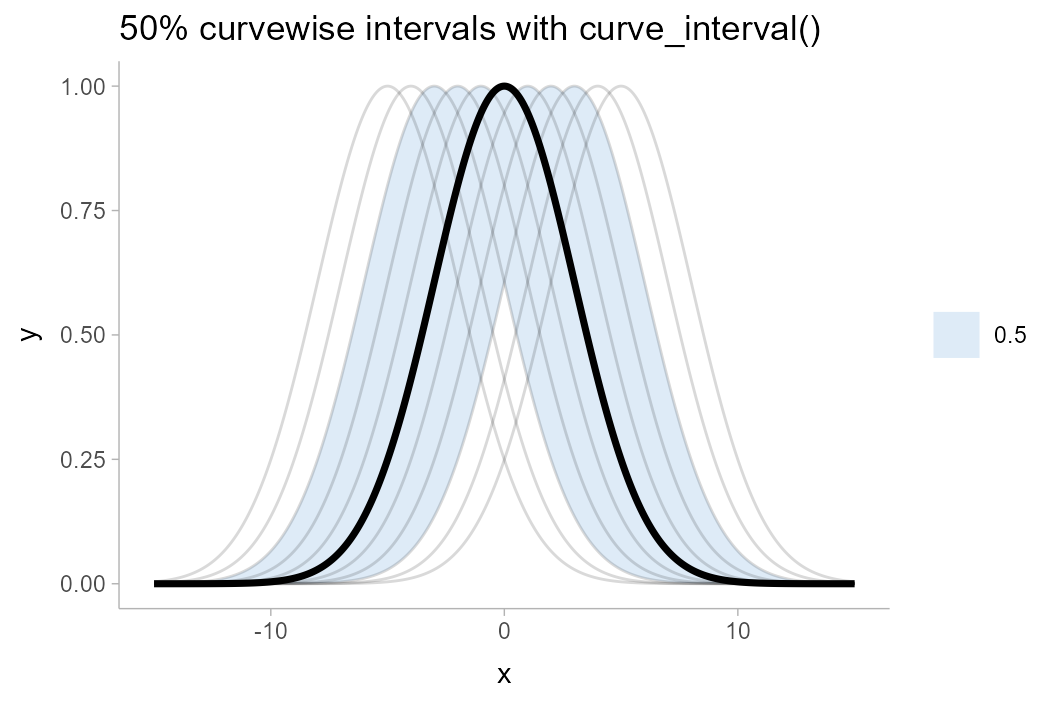

Note how the 50% curvewise interval now contains half of the underlying curves, and the median curve is one of the underlying curves (so it is more representative of the curve shape we should expect). These intervals also cover the peaks of the curves, where the pointwise intervals did not.

An X% curvewise interval is calculated across all the curves by taking the top X% closest curves to the central curve, for some definition of “close” and “central”. The curve_interval() function currently orders curves by mean halfspace depth, which is basically how close each curve is to the pointwise median in percentiles, on average.

Given the above, let’s see what more realistic curvewise intervals of the above example might look like by using a larger number of draws:

k = 1000 # number of curves
large_df = tibble(
  .draw = 1:k,
  mean = seq(-5,5, length.out = k),
  x = list(seq(-15,15,length.out = n))
) %>%
  unnest(x) %>%
  mutate(y = dnorm(x, mean, 3)/max(dnorm(x, mean, 3)))

pointwise_plot = large_df %>%
  group_by(x) %>%
  median_qi(y, .width = c(.5, .8, .95)) %>%
  ggplot(aes(x = x, y = y)) +
  geom_hline(yintercept = 1, color = "gray75", linetype = "dashed") +
  geom_lineribbon(aes(ymin = .lower, ymax = .upper)) +
  scale_fill_brewer() +
  ggtitle("point_interval()")

curvewise_plot = large_df %>%
  group_by(x) %>%
  curve_interval(y, .width = c(.5, .8, .95)) %>%
  ggplot(aes(x = x, y = y)) +
  geom_hline(yintercept = 1, color = "gray75", linetype = "dashed") +
  geom_lineribbon(aes(ymin = .lower, ymax = .upper)) +
  scale_fill_brewer() +
  ggtitle("curve_interval()")

pointwise_plot / curvewise_plot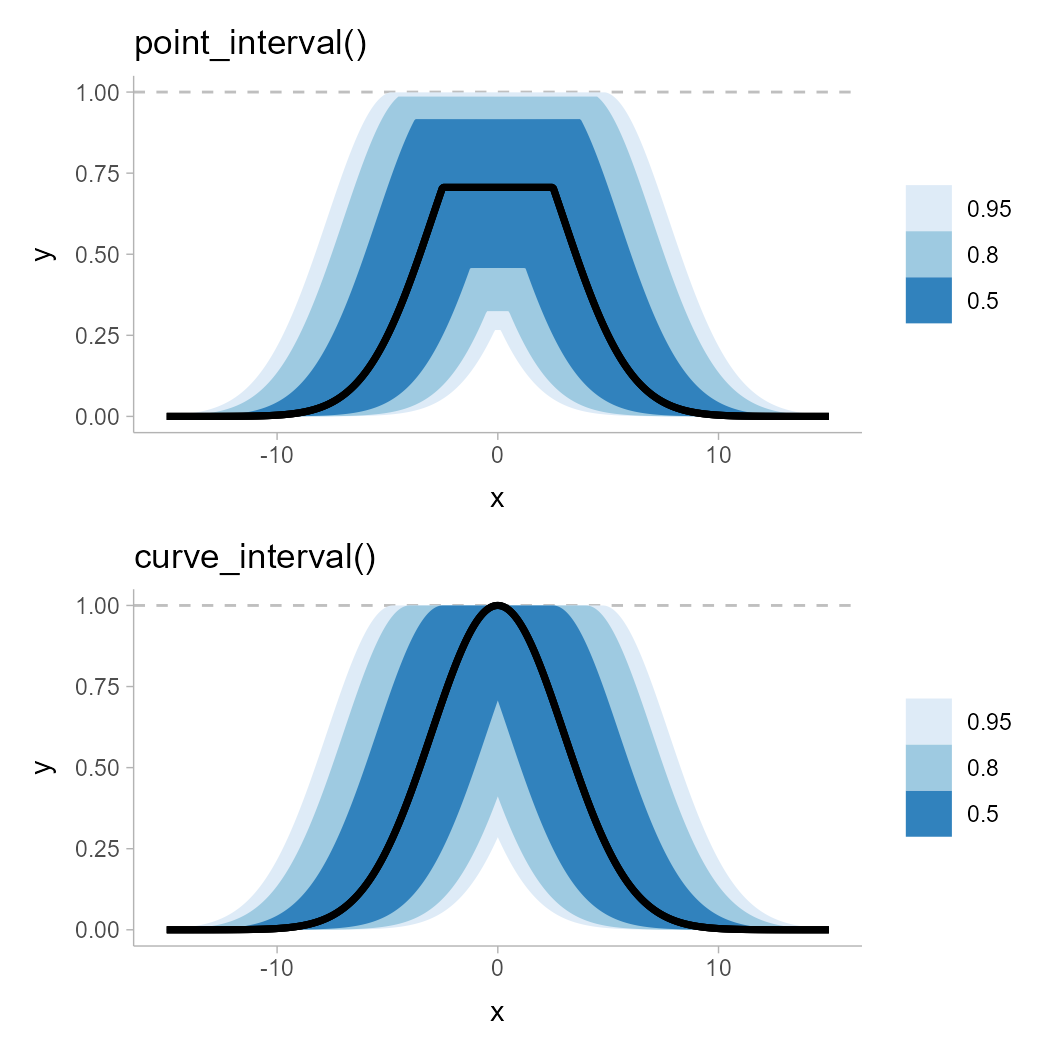

Notice how the pointwise intervals miss out on the peaks of this distribution of curves. Even the 95% ribbon, which appears to reach up to the peaks, in fact falls slightly short. While this is a bit of a pathological example, it does demonstrate the potential shortcomings of pointwise intervals.

Limitations of curvewise intervals

One challenge with curvewise intervals is that they can tend to be very conservative, especially at moderate-to-large intervals widths. Let’s bootstrap some LOESS fits to horsepower versus MPG in the mtcars dataset:

set.seed(1234)
n = 4000
mpg = seq(min(mtcars$mpg), max(mtcars$mpg), length.out = 100)

mtcars_boot = tibble(
  .draw = 1:n,
  m = lapply(.draw, function(d) loess(
    hp ~ mpg,
    span = 0.9,
    # this lets us predict outside the range of the data
    control = loess.control(surface = "direct"),
    data = slice_sample(mtcars, prop = 1, replace = TRUE)
  )),
  hp = lapply(m, predict, newdata = tibble(mpg)),
  mpg = list(mpg)
) %>%
  select(-m) %>%
  unnest(c(hp, mpg))

This is a pretty naive approach, and definitely not a great way of analyzing this data, but it will illustrate the problems of some kinds of problems we might get with joint intervals. Let’s look at a spaghetti plot of just 400 draws from this bootstrap distribution first:

mtcars_boot %>%
  filter(.draw < 400) %>%
  ggplot(aes(x = mpg, y = hp)) +
  geom_line(aes(group = .draw), alpha = 1/10) +
  geom_point(data = mtcars) +
  coord_cartesian(ylim = c(0, 400))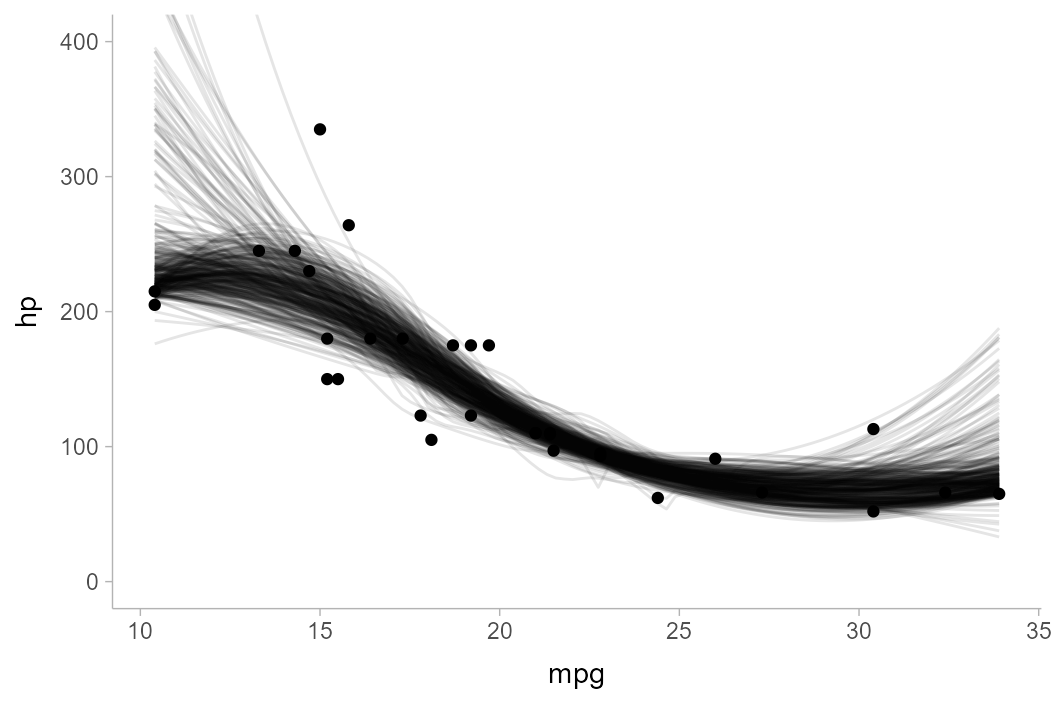

Now, pointwise intervals:

mtcars_boot %>%
  ggplot(aes(x = mpg, y = hp)) +
  stat_lineribbon(.width = c(.5, .7, .9)) +
  geom_point(data = mtcars) +
  scale_fill_brewer() +
  coord_cartesian(ylim = c(0, 400))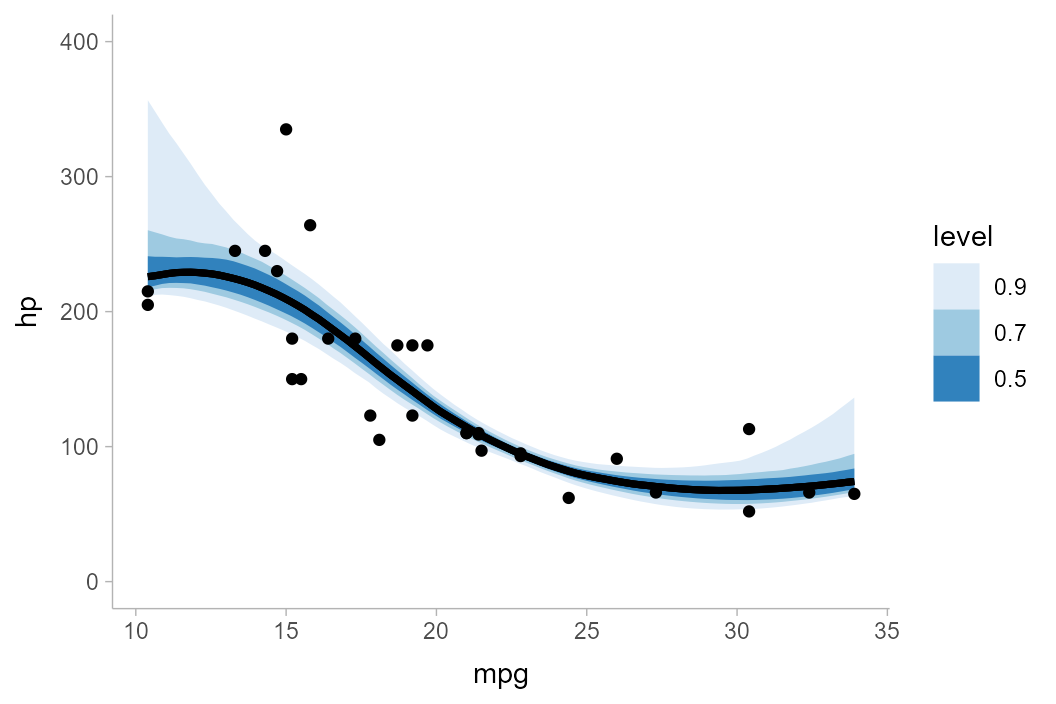

Finally, curvewise intervals:

mtcars_boot %>%
  group_by(mpg) %>%
  curve_interval(hp, .width = c(.5, .7, .9)) %>%
  ggplot(aes(x = mpg, y = hp)) +
  geom_lineribbon(aes(ymin = .lower, ymax = .upper)) +
  geom_point(data = mtcars) +
  scale_fill_brewer() +
  coord_cartesian(ylim = c(0, 400))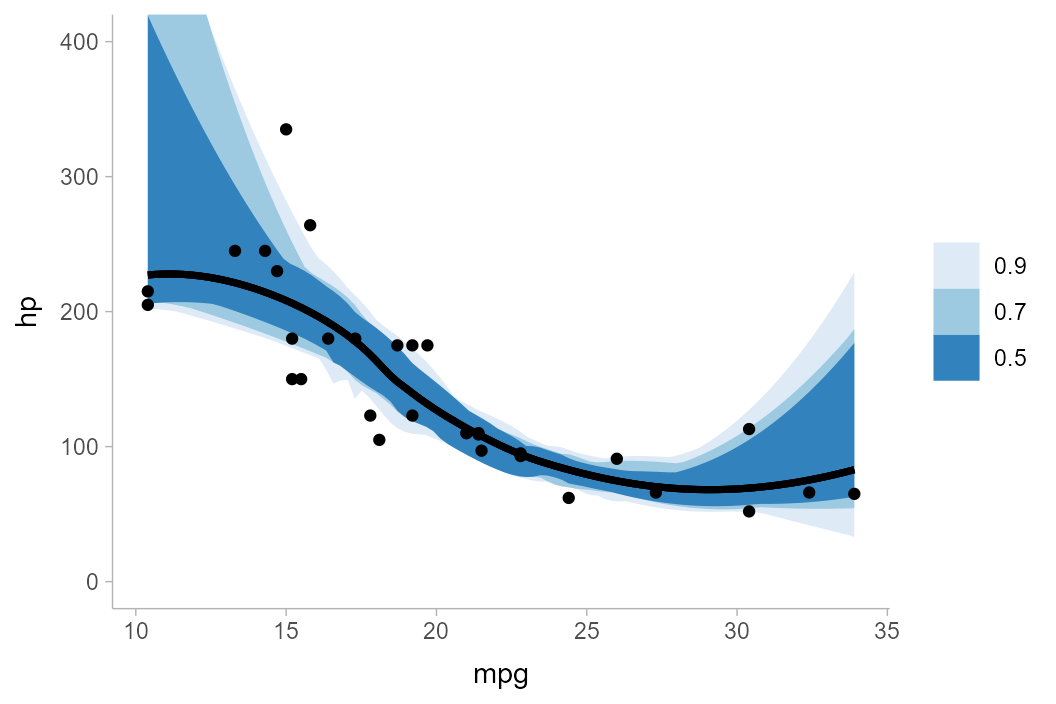

Notice how noisy the curvewise intervals are. In addition, because a number of curves tend to start low and end high (or vice versa), above 50%, the bands rapidly expand to cover almost all of the curves in the sample, regardless of coverage level. You can try different methods to sometimes get improved bands; e.g. using the "bd-mbd" method per Sun and Genton (2011) works better on this dataset:

mtcars_boot %>%
  group_by(mpg) %>%
  curve_interval(hp, .width = c(.5, .7, .9), .interval = "bd-mbd") %>%
  ggplot(aes(x = mpg, y = hp)) +
  geom_lineribbon(aes(ymin = .lower, ymax = .upper)) +
  geom_point(data = mtcars) +
  scale_fill_brewer() +
  coord_cartesian(ylim = c(0, 400))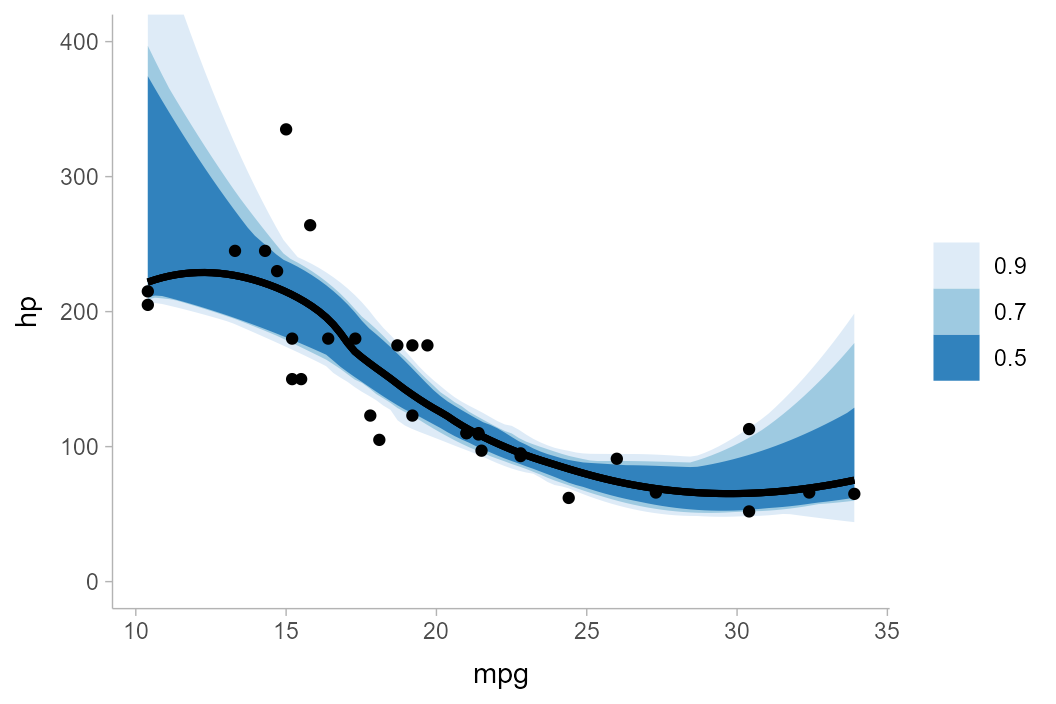

In general I have found that there is no one method that consistently works well on all datasets. No matter the method, intervals often become problematic above 50%, hence the default .width for curve_interval() is 0.5 (unlike the default for point_interval(), which is 0.95). In any case, caution when using these intervals is advised.

Matthew Kay

2024-03-03