Add draws from the posterior fit, predictions, or residuals of a model to a data frame

Source: R/epred_draws.R, R/linpred_draws.R, R/predicted_draws.R, and 1 more

Given a data frame and a model, adds draws from the linear/link-level predictor, the expectation of the posterior predictive, the posterior predictive, or the residuals of a model to the data frame in a long format.

add_epred_draws(
  newdata,
  object,
  ...,
  value = ".epred",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category",
  dpar = NULL
)

epred_draws(
  object,
  newdata,
  ...,
  value = ".epred",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category",
  dpar = NULL
)

# Default S3 method
epred_draws(
  object,
  newdata,
  ...,
  value = ".epred",
  seed = NULL,
  category = NULL
)

# S3 method for class 'stanreg'
epred_draws(
  object,
  newdata,
  ...,
  value = ".epred",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category",
  dpar = NULL
)

# S3 method for class 'brmsfit'
epred_draws(
  object,
  newdata,
  ...,
  value = ".epred",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category",
  dpar = NULL
)

add_linpred_draws(
  newdata,
  object,
  ...,
  value = ".linpred",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category",
  dpar = NULL,
  n
)

linpred_draws(
  object,
  newdata,
  ...,
  value = ".linpred",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category",
  dpar = NULL,
  n,
  scale
)

# Default S3 method
linpred_draws(
  object,
  newdata,
  ...,
  value = ".linpred",
  seed = NULL,
  category = NULL
)

# S3 method for class 'stanreg'
linpred_draws(
  object,
  newdata,
  ...,
  value = ".linpred",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category",
  dpar = NULL
)

# S3 method for class 'brmsfit'
linpred_draws(
  object,
  newdata,
  ...,
  value = ".linpred",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category",
  dpar = NULL
)

add_predicted_draws(
  newdata,
  object,
  ...,
  value = ".prediction",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category",
  n
)

predicted_draws(
  object,
  newdata,
  ...,
  value = ".prediction",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category",
  n,
  prediction
)

# Default S3 method
predicted_draws(
  object,
  newdata,
  ...,
  value = ".prediction",
  seed = NULL,
  category = ".category"
)

# S3 method for class 'stanreg'
predicted_draws(
  object,
  newdata,
  ...,
  value = ".prediction",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category"
)

# S3 method for class 'brmsfit'
predicted_draws(
  object,
  newdata,
  ...,
  value = ".prediction",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category"
)

add_residual_draws(
  newdata,
  object,
  ...,
  value = ".residual",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category",
  n
)

residual_draws(
  object,
  newdata,
  ...,
  value = ".residual",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category",
  n,
  residual
)

# Default S3 method
residual_draws(object, newdata, ...)

# S3 method for class 'brmsfit'
residual_draws(
  object,
  newdata,
  ...,
  value = ".residual",
  ndraws = NULL,
  seed = NULL,
  re_formula = NULL,
  category = ".category"
)

Arguments

newdata

Data frame to generate predictions from.

object

A supported Bayesian model fit that can provide fits and predictions. Supported models are listed in the second section of tidybayes-models: Models Supporting Prediction. While other functions in this package (like spread_draws()) support a wider range of models, to work with add_epred_draws(), add_predicted_draws(), etc. a model must provide an interface for generating predictions, thus more generic Bayesian modeling interfaces like runjags and rstan are not directly supported for these functions (only wrappers around those languages that provide predictions, like rstanarm and brm, are supported here).

...

Additional arguments passed to the underlying prediction method for the type of model given.

value

The name of the output column:

  • for [add_]epred_draws(), defaults to ".epred".

  • for [add_]predicted_draws(), defaults to ".prediction".

  • for [add_]linpred_draws(), defaults to ".linpred".

  • for [add_]residual_draws(), defaults to ".residual"

ndraws

The number of draws to return, or NULL to return all draws.

seed

A seed to use when subsampling draws (i.e. when ndraws is not NULL).

re_formula

formula containing group-level effects to be considered in the prediction. If NULL (default), include all group-level effects; if NA, include no group-level effects. Some model types (such as brms::brmsfit and rstanarm::stanreg-objects) allow marginalizing over grouping factors by specifying new levels of a factor in newdata. In the case of brms::brm(), you must also pass allow_new_levels = TRUE here to include new levels (see brms::posterior_predict()).

category

For some ordinal, multinomial, and multivariate models (notably, brms::brm() models but not rstanarm::stan_polr() models), multiple sets of rows will be returned per input row for epred_draws() or predicted_draws(), depending on the model type. For ordinal/multinomial models, these rows correspond to different categories of the response variable. For multivariate models, these correspond to different response variables. The category argument specifies the name of the column to put the category names (or variable names) into in the resulting data frame. The default name of this column (".category") reflects the fact that this functionality was originally used only for ordinal models and has been re-used for multivariate models. The fact that multiple rows per response are returned only for some model types reflects the fact that tidybayes takes the approach of tidying whatever output is given to us, and the output from different modeling functions differs on this point. See vignette("tidy-brms") and vignette("tidy-rstanarm") for examples of dealing with output from ordinal models using both approaches.

dpar

For add_epred_draws() and add_linpred_draws(): Should distributional regression parameters be included in the output? Valid only for models that support distributional regression parameters, such as submodels for variance parameters (as in brms::brm()). If TRUE, distributional regression parameters are included in the output as additional columns named after each parameter (alternative names can be provided using a list or named vector, e.g. c(sigma.hat = "sigma") would output the "sigma" parameter from a model as a column named "sigma.hat"). If NULL or FALSE (the default), distributional regression parameters are not included.

n

(Deprecated). Use ndraws.

scale

(Deprecated). Use the appropriate function (epred_draws() or linpred_draws()) depending on what type of distribution you want. For linpred_draws(), you may want the transform argument. See rstanarm::posterior_linpred() or brms::posterior_linpred().

prediction, residual

(Deprecated). Use value.

Value

A data frame (actually, a tibble) with a .row column (a factor grouping rows from the input newdata), .chain column (the chain each draw came from, or NA if the model does not provide chain information), .iteration column (the iteration the draw came from, or NA if the model does not provide iteration information), and a .draw column (a unique index corresponding to each draw from the distribution). In addition, epred_draws includes a column with its name specified by the epred argument (default ".epred"); linpred_draws includes a column with its name specified by the linpred argument (default ".linpred"), and predicted_draws contains a column with its name specified by the .prediction argument (default ".prediction"). For convenience, the resulting data frame comes grouped by the original input rows.

Details

Consider a model like:

$$\begin{array}{rcl} y &\sim& \textrm{SomeDist}(\theta_1, \theta_2)\\ f_1(\theta_1) &=& \alpha_1 + \beta_1 x\\ f_2(\theta_2) &=& \alpha_2 + \beta_2 x \end{array}$$

This model has:

  • an outcome variable, \(y\)

  • a response distribution, \(\textrm{SomeDist}\), having parameters \(\theta_1\) (with link function \(f_1\)) and \(\theta_2\) (with link function \(f_2\))

  • a single predictor, \(x\)

  • coefficients \(\alpha_1\), \(\beta_1\), \(\alpha_2\), and \(\beta_2\)

We fit this model to some observed data, \(y_\textrm{obs}\), and predictors, \(x_\textrm{obs}\). Given new values of predictors, \(x_\textrm{new}\), supplied in the data frame newdata, the functions for posterior draws are defined as follows:

  • add_predicted_draws() adds draws from the posterior predictive distribution, \(p(y_\textrm{new} | x_\textrm{new}, y_\textrm{obs})\), to the data. It corresponds to rstanarm::posterior_predict() or brms::posterior_predict().

  • add_epred_draws() adds draws from the expectation of the posterior predictive distribution, aka the conditional expectation, \(E(y_\textrm{new} | x_\textrm{new}, y_\textrm{obs})\), to the data. It corresponds to rstanarm::posterior_epred() or brms::posterior_epred(). Not all models support this function.

  • add_linpred_draws() adds draws from the posterior linear predictors to the data. It corresponds to rstanarm::posterior_linpred() or brms::posterior_linpred(). Depending on the model type and additional parameters passed, this may be:

    • The untransformed linear predictor, e.g. \(p(f_1(\theta_1) | x_\textrm{new}, y_\textrm{obs})\) = \(p(\alpha_1 + \beta_1 x_\textrm{new} | x_\textrm{new}, y_\textrm{obs})\). This is returned by add_linpred_draws(transform = FALSE) for brms and rstanarm models. It is analogous to type = "link" in predict.glm().

    • The inverse-link transformed linear predictor, e.g. \(p(\theta_1 | x_\textrm{new}, y_\textrm{obs})\) = \(p(f_1^{-1}(\alpha_1 + \beta_1 x_\textrm{new}) | x_\textrm{new}, y_\textrm{obs})\). This is returned by add_linpred_draws(transform = TRUE) for brms and rstanarm models. It is analogous to type = "response" in predict.glm().

    NOTE: add_linpred_draws(transform = TRUE) and add_epred_draws() may be equivalent but are not guaranteed to be. They are equivalent when the expectation of the response distribution is equal to its first parameter, i.e. when \(E(y) = \theta_1\). Many distributions have this property (e.g. Normal distributions, Bernoulli distributions), but not all. If you want the expectation of the posterior predictive, it is best to use add_epred_draws() if available, and if not available, verify this property holds prior to using add_linpred_draws().

  • add_residual_draws() adds draws from residuals, \(p(y_\textrm{obs} - y_\textrm{new} | x_\textrm{new}, y_\textrm{obs})\), to the data. It corresponds to brms::residuals.brmsfit().

The corresponding functions without add_ as a prefix are alternate spellings with the opposite order of the first two arguments: e.g. add_predicted_draws(newdata, object) versus predicted_draws(object, newdata). This facilitates use in data processing pipelines that start either with a data frame or a model.

Given equal choice between the two, the spellings prefixed with add_ are preferred.

See also

add_draws() for the variant of these functions for use with packages that do not have explicit support for these functions yet. See spread_draws() for manipulating posteriors directly.

Author

Matthew Kay

Examples

# \dontrun{

library(ggplot2)
library(dplyr)
library(brms)
library(modelr)

theme_set(theme_light())

m_mpg = brm(mpg ~ hp * cyl, data = mtcars,
  # 1 chain / few iterations just so example runs quickly
  # do not use in practice
  chains = 1, iter = 500)
#> Compiling Stan program...
#> Start sampling
#> 
#> SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
#> Chain 1: 
#> Chain 1: Gradient evaluation took 4.3e-05 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.43 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 1: 
#> Chain 1: 
#> Chain 1: Iteration:   1 / 500 [  0%]  (Warmup)
#> Chain 1: Iteration:  50 / 500 [ 10%]  (Warmup)
#> Chain 1: Iteration: 100 / 500 [ 20%]  (Warmup)
#> Chain 1: Iteration: 150 / 500 [ 30%]  (Warmup)
#> Chain 1: Iteration: 200 / 500 [ 40%]  (Warmup)
#> Chain 1: Iteration: 250 / 500 [ 50%]  (Warmup)
#> Chain 1: Iteration: 251 / 500 [ 50%]  (Sampling)
#> Chain 1: Iteration: 300 / 500 [ 60%]  (Sampling)
#> Chain 1: Iteration: 350 / 500 [ 70%]  (Sampling)
#> Chain 1: Iteration: 400 / 500 [ 80%]  (Sampling)
#> Chain 1: Iteration: 450 / 500 [ 90%]  (Sampling)
#> Chain 1: Iteration: 500 / 500 [100%]  (Sampling)
#> Chain 1: 
#> Chain 1:  Elapsed Time: 0.123 seconds (Warm-up)
#> Chain 1:                0.047 seconds (Sampling)
#> Chain 1:                0.17 seconds (Total)
#> Chain 1: 
#> Warning: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
#> Running the chains for more iterations may help. See
#> https://mc-stan.org/misc/warnings.html#bulk-ess
#> Warning: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
#> Running the chains for more iterations may help. See
#> https://mc-stan.org/misc/warnings.html#tail-ess

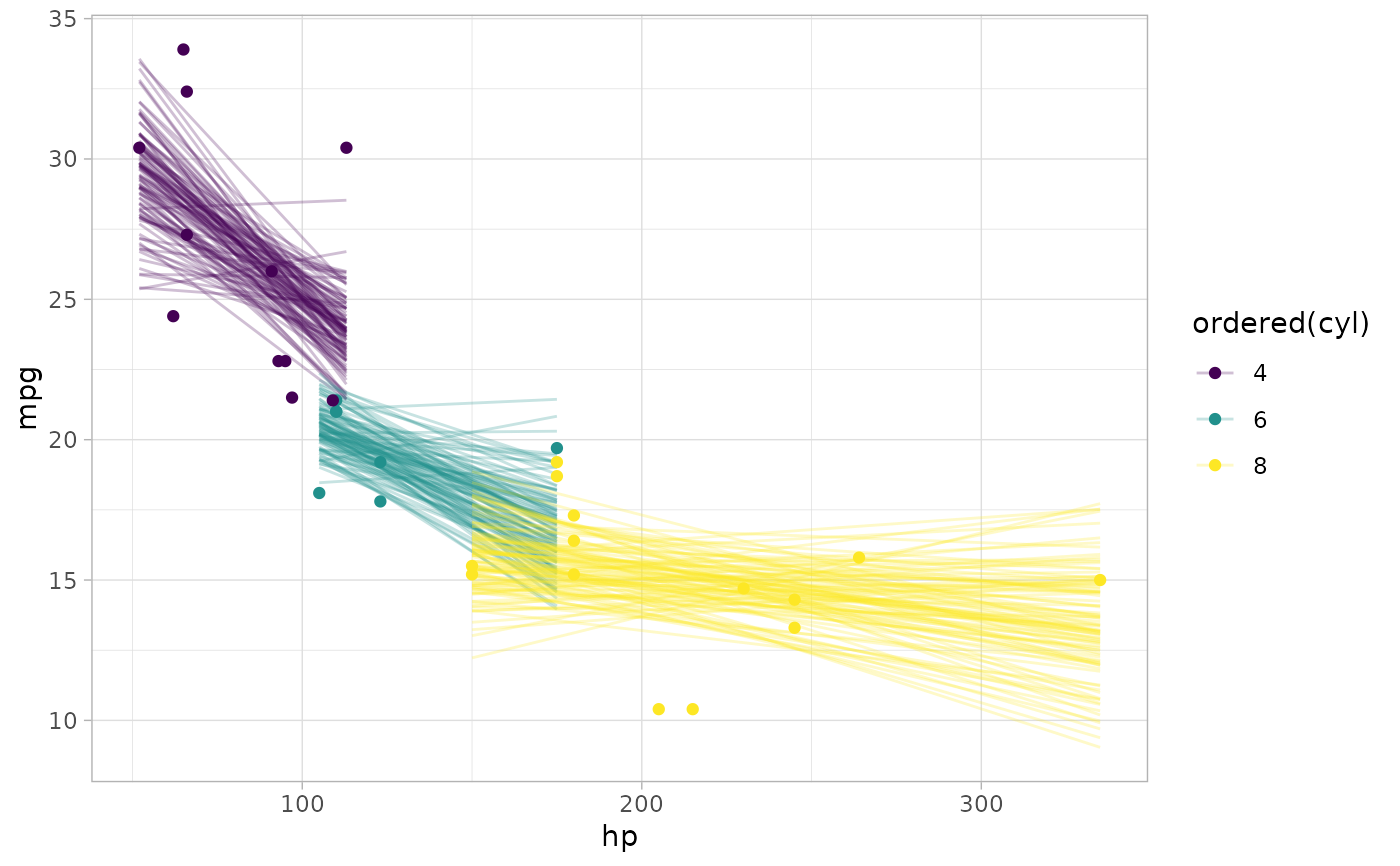
# draw 100 lines from the posterior means and overplot them
mtcars %>%
  group_by(cyl) %>%
  data_grid(hp = seq_range(hp, n = 101)) %>%
  # NOTE: only use ndraws here when making spaghetti plots; for
  # plotting intervals it is always best to use all draws (omit ndraws)
  add_epred_draws(m_mpg, ndraws = 100) %>%
  ggplot(aes(x = hp, y = mpg, color = ordered(cyl))) +
  geom_line(aes(y = .epred, group = paste(cyl, .draw)), alpha = 0.25) +
  geom_point(data = mtcars)


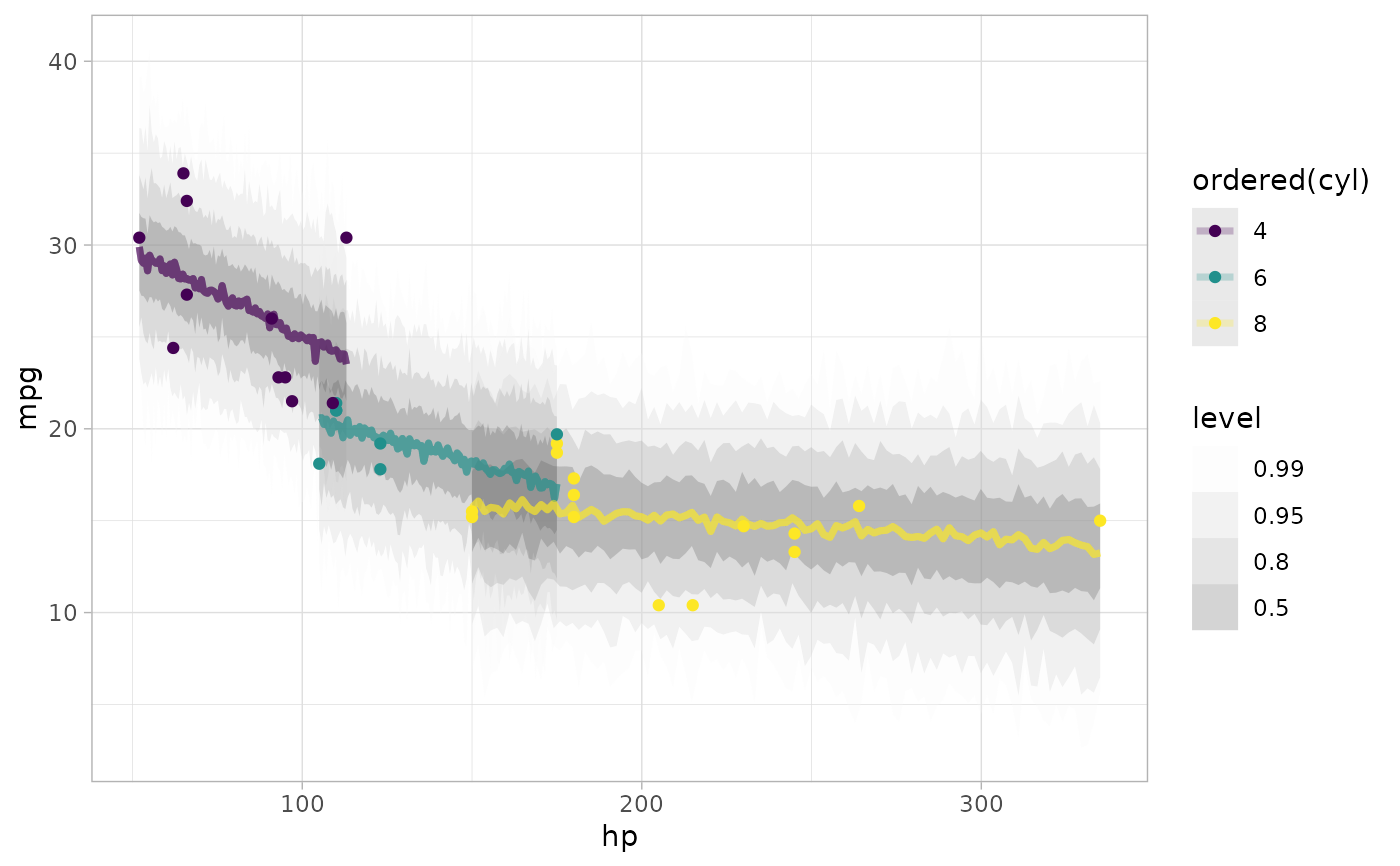
# plot posterior predictive intervals
mtcars %>%
  group_by(cyl) %>%
  data_grid(hp = seq_range(hp, n = 101)) %>%
  add_predicted_draws(m_mpg) %>%
  ggplot(aes(x = hp, y = mpg, color = ordered(cyl))) +
  stat_lineribbon(aes(y = .prediction), .width = c(.99, .95, .8, .5), alpha = 0.25) +
  geom_point(data = mtcars) +
  scale_fill_brewer(palette = "Greys")


# }