Add rvars for the linear predictor, posterior expectation, posterior predictive, or residuals of a model to a data frame
Source: R/epred_rvars.R, R/linpred_rvars.R, R/predicted_rvars.R
add_predicted_rvars.RdGiven a data frame and a model, adds rvars of draws from the linear/link-level predictor,
the expectation of the posterior predictive, or the posterior predictive to
the data frame.
add_epred_rvars(
newdata,
object,
...,
value = ".epred",
ndraws = NULL,
seed = NULL,
re_formula = NULL,
dpar = NULL,
columns_to = NULL
)
epred_rvars(
object,
newdata,
...,
value = ".epred",
ndraws = NULL,
seed = NULL,
re_formula = NULL,
dpar = NULL,
columns_to = NULL
)
# Default S3 method
epred_rvars(
object,
newdata,
...,
value = ".epred",
seed = NULL,
dpar = NULL,
columns_to = NULL
)
# S3 method for class 'stanreg'
epred_rvars(
object,
newdata,
...,
value = ".epred",
ndraws = NULL,
seed = NULL,
re_formula = NULL,
dpar = NULL,
columns_to = NULL
)
# S3 method for class 'brmsfit'
epred_rvars(
object,
newdata,
...,
value = ".epred",
ndraws = NULL,
seed = NULL,
re_formula = NULL,
dpar = NULL,
columns_to = NULL
)
add_linpred_rvars(
newdata,
object,
...,
value = ".linpred",
ndraws = NULL,
seed = NULL,
re_formula = NULL,
dpar = NULL,
columns_to = NULL
)
linpred_rvars(
object,
newdata,
...,
value = ".linpred",
ndraws = NULL,
seed = NULL,
re_formula = NULL,
dpar = NULL,
columns_to = NULL
)
# Default S3 method
linpred_rvars(
object,
newdata,
...,
value = ".linpred",
seed = NULL,
dpar = NULL,
columns_to = NULL
)
# S3 method for class 'stanreg'
linpred_rvars(
object,
newdata,
...,
value = ".linpred",
ndraws = NULL,
seed = NULL,
re_formula = NULL,
dpar = NULL,
columns_to = NULL
)
# S3 method for class 'brmsfit'
linpred_rvars(
object,
newdata,
...,
value = ".linpred",
ndraws = NULL,
seed = NULL,
re_formula = NULL,
dpar = NULL,
columns_to = NULL
)
add_predicted_rvars(
newdata,
object,
...,
value = ".prediction",
ndraws = NULL,
seed = NULL,
re_formula = NULL,
columns_to = NULL
)
predicted_rvars(
object,
newdata,
...,
value = ".prediction",
ndraws = NULL,
seed = NULL,
re_formula = NULL,
columns_to = NULL
)
# Default S3 method
predicted_rvars(
object,
newdata,
...,
value = ".prediction",
seed = NULL,
columns_to = NULL
)
# S3 method for class 'stanreg'
predicted_rvars(
object,
newdata,
...,
value = ".prediction",
ndraws = NULL,
seed = NULL,
re_formula = NULL,
columns_to = NULL
)
# S3 method for class 'brmsfit'
predicted_rvars(
object,
newdata,
...,
value = ".prediction",
ndraws = NULL,
seed = NULL,
re_formula = NULL,
columns_to = NULL
)Arguments
- newdata
Data frame to generate predictions from.
- object
A supported Bayesian model fit that can provide fits and predictions. Supported models are listed in the second section of tidybayes-models: Models Supporting Prediction. While other functions in this package (like
spread_rvars()) support a wider range of models, to work withadd_epred_rvars(),add_predicted_rvars(), etc. a model must provide an interface for generating predictions, thus more generic Bayesian modeling interfaces likerunjagsandrstanare not directly supported for these functions (only wrappers around those languages that provide predictions, likerstanarmandbrm, are supported here).- ...
Additional arguments passed to the underlying prediction method for the type of model given.
- value
The name of the output column:
for
[add_]epred_rvars(), defaults to".epred".for
[add_]predicted_rvars(), defaults to".prediction".for
[add_]linpred_rvars(), defaults to".linpred".
- ndraws
The number of draws to return, or
NULLto return all draws.- seed
A seed to use when subsampling draws (i.e. when
ndrawsis notNULL).- re_formula
formula containing group-level effects to be considered in the prediction. If
NULL(default), include all group-level effects; ifNA, include no group-level effects. Some model types (such as brms::brmsfit and rstanarm::stanreg-objects) allow marginalizing over grouping factors by specifying new levels of a factor innewdata. In the case ofbrms::brm(), you must also passallow_new_levels = TRUEhere to include new levels (seebrms::posterior_predict()).- dpar
For
add_epred_rvars()andadd_linpred_rvars(): Should distributional regression parameters be included in the output? Valid only for models that support distributional regression parameters, such as submodels for variance parameters (as inbrms::brm()). IfTRUE, distributional regression parameters are included in the output as additional columns named after each parameter (alternative names can be provided using a list or named vector, e.g.c(sigma.hat = "sigma")would output the"sigma"parameter from a model as a column named"sigma.hat"). IfNULLorFALSE(the default), distributional regression parameters are not included.- columns_to
For some models, such as ordinal, multinomial, and multivariate models (notably,
brms::brm()models but notrstanarm::stan_polr()models), the column of predictions in the resulting data frame may include nested columns. For example, for ordinal/multinomial models, these columns correspond to different categories of the response variable. It may be more convenient to turn these nested columns into rows in the output; if this is desired, setcolumns_toto a string representing the name of a column you would like the column names to be placed in. In this case, a.rowcolumn will also be added to the result indicating which rows of the output correspond to the same row innewdata. Seevignette("tidy-posterior")for examples of dealing with output ordinal models.
Value
A data frame (actually, a tibble) equal to the input newdata with
additional columns added containing rvars representing the requested predictions or fits.
Details
Consider a model like:
$$\begin{array}{rcl} y &\sim& \textrm{SomeDist}(\theta_1, \theta_2)\\ f_1(\theta_1) &=& \alpha_1 + \beta_1 x\\ f_2(\theta_2) &=& \alpha_2 + \beta_2 x \end{array}$$
This model has:
an outcome variable, \(y\)
a response distribution, \(\textrm{SomeDist}\), having parameters \(\theta_1\) (with link function \(f_1\)) and \(\theta_2\) (with link function \(f_2\))
a single predictor, \(x\)
coefficients \(\alpha_1\), \(\beta_1\), \(\alpha_2\), and \(\beta_2\)
We fit this model to some observed data, \(y_\textrm{obs}\), and predictors,
\(x_\textrm{obs}\). Given new values of predictors, \(x_\textrm{new}\),
supplied in the data frame newdata, the functions for posterior draws are
defined as follows:
add_predicted_rvars()addsrvars containing draws from the posterior predictive distribution, \(p(y_\textrm{new} | x_\textrm{new}, y_\textrm{obs})\), to the data. It corresponds torstanarm::posterior_predict()orbrms::posterior_predict().add_epred_rvars()addsrvars containing draws from the expectation of the posterior predictive distribution, aka the conditional expectation, \(E(y_\textrm{new} | x_\textrm{new}, y_\textrm{obs})\), to the data. It corresponds torstanarm::posterior_epred()orbrms::posterior_epred(). Not all models support this function.add_linpred_rvars()addsrvars containing draws from the posterior linear predictors to the data. It corresponds torstanarm::posterior_linpred()orbrms::posterior_linpred(). Depending on the model type and additional parameters passed, this may be:The untransformed linear predictor, e.g. \(p(f_1(\theta_1) | x_\textrm{new}, y_\textrm{obs})\) = \(p(\alpha_1 + \beta_1 x_\textrm{new} | x_\textrm{new}, y_\textrm{obs})\). This is returned by
add_linpred_rvars(transform = FALSE)for brms and rstanarm models. It is analogous totype = "link"inpredict.glm().The inverse-link transformed linear predictor, e.g. \(p(\theta_1 | x_\textrm{new}, y_\textrm{obs})\) = \(p(f_1^{-1}(\alpha_1 + \beta_1 x_\textrm{new}) | x_\textrm{new}, y_\textrm{obs})\). This is returned by
add_linpred_rvars(transform = TRUE)for brms and rstanarm models. It is analogous totype = "response"inpredict.glm().
NOTE:
add_linpred_rvars(transform = TRUE)andadd_epred_rvars()may be equivalent but are not guaranteed to be. They are equivalent when the expectation of the response distribution is equal to its first parameter, i.e. when \(E(y) = \theta_1\). Many distributions have this property (e.g. Normal distributions, Bernoulli distributions), but not all. If you want the expectation of the posterior predictive, it is best to useadd_epred_rvars()if available, and if not available, verify this property holds prior to usingadd_linpred_rvars().
The corresponding functions without add_ as a prefix are alternate spellings
with the opposite order of the first two arguments: e.g. add_predicted_rvars(newdata, object)
versus predicted_rvars(object, newdata). This facilitates use in data
processing pipelines that start either with a data frame or a model.
Given equal choice between the two, the spellings prefixed with add_
are preferred.
See also
add_predicted_draws() for the analogous functions that use a long-data-frame-of-draws
format instead of a data-frame-of-rvars format. See spread_rvars() for manipulating posteriors directly.
Examples
# \dontrun{
library(ggplot2)
library(dplyr)
library(posterior)
#> This is posterior version 1.6.0
#>
#> Attaching package: 'posterior'
#> The following objects are masked from 'package:stats':
#>
#> mad, sd, var
#> The following objects are masked from 'package:base':
#>
#> %in%, match
library(brms)
library(modelr)
theme_set(theme_light())
m_mpg = brm(mpg ~ hp * cyl, data = mtcars, family = lognormal(),
# 1 chain / few iterations just so example runs quickly
# do not use in practice
chains = 1, iter = 500)
#> Compiling Stan program...
#> Start sampling
#>
#> SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
#> Chain 1:
#> Chain 1: Gradient evaluation took 3.8e-05 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.38 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 1:
#> Chain 1:
#> Chain 1: Iteration: 1 / 500 [ 0%] (Warmup)
#> Chain 1: Iteration: 50 / 500 [ 10%] (Warmup)
#> Chain 1: Iteration: 100 / 500 [ 20%] (Warmup)
#> Chain 1: Iteration: 150 / 500 [ 30%] (Warmup)
#> Chain 1: Iteration: 200 / 500 [ 40%] (Warmup)
#> Chain 1: Iteration: 250 / 500 [ 50%] (Warmup)
#> Chain 1: Iteration: 251 / 500 [ 50%] (Sampling)
#> Chain 1: Iteration: 300 / 500 [ 60%] (Sampling)
#> Chain 1: Iteration: 350 / 500 [ 70%] (Sampling)
#> Chain 1: Iteration: 400 / 500 [ 80%] (Sampling)
#> Chain 1: Iteration: 450 / 500 [ 90%] (Sampling)
#> Chain 1: Iteration: 500 / 500 [100%] (Sampling)
#> Chain 1:
#> Chain 1: Elapsed Time: 0.576 seconds (Warm-up)
#> Chain 1: 0.577 seconds (Sampling)
#> Chain 1: 1.153 seconds (Total)
#> Chain 1:
#> Warning: There were 1 transitions after warmup that exceeded the maximum treedepth. Increase max_treedepth above 10. See
#> https://mc-stan.org/misc/warnings.html#maximum-treedepth-exceeded
#> Warning: Examine the pairs() plot to diagnose sampling problems
#> Warning: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
#> Running the chains for more iterations may help. See
#> https://mc-stan.org/misc/warnings.html#bulk-ess
#> Warning: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
#> Running the chains for more iterations may help. See
#> https://mc-stan.org/misc/warnings.html#tail-ess
# Look at mean predictions for some cars (epred) and compare to
# the exponeniated mu parameter of the lognormal distribution (linpred).
# Notice how they are NOT the same. This is because exp(mu) for a
# lognormal distribution is equal to its median, not its mean.
mtcars %>%
select(hp, cyl, mpg) %>%
add_epred_rvars(m_mpg) %>%
add_linpred_rvars(m_mpg, value = "mu") %>%
mutate(expmu = exp(mu), .epred - expmu)
#> # A tibble: 32 × 7
#> hp cyl mpg .epred mu expmu `.epred - expmu`
#> <dbl> <dbl> <dbl> <rvar[1d]> <rvar[1d]> <rvar[1d]> <rvar[1d]>
#> 1 110 6 21 20 ± 0.92 3.0 ± 0.045 20 ± 0.90 0.26 ± 0.069
#> 2 110 6 21 20 ± 0.92 3.0 ± 0.045 20 ± 0.90 0.26 ± 0.069
#> 3 93 4 22.8 26 ± 1.28 3.2 ± 0.049 26 ± 1.25 0.34 ± 0.088
#> 4 110 6 21.4 20 ± 0.92 3.0 ± 0.045 20 ± 0.90 0.26 ± 0.069
#> 5 175 8 18.7 16 ± 0.73 2.7 ± 0.046 15 ± 0.71 0.20 ± 0.053
#> 6 105 6 18.1 20 ± 0.93 3.0 ± 0.045 20 ± 0.91 0.26 ± 0.070
#> 7 245 8 14.3 15 ± 0.81 2.7 ± 0.055 15 ± 0.80 0.19 ± 0.050
#> 8 62 4 24.4 29 ± 1.86 3.3 ± 0.065 28 ± 1.84 0.37 ± 0.094
#> 9 95 4 22.8 26 ± 1.31 3.2 ± 0.050 26 ± 1.28 0.33 ± 0.088
#> 10 123 6 19.2 20 ± 0.96 3.0 ± 0.048 19 ± 0.93 0.25 ± 0.068
#> # ℹ 22 more rows
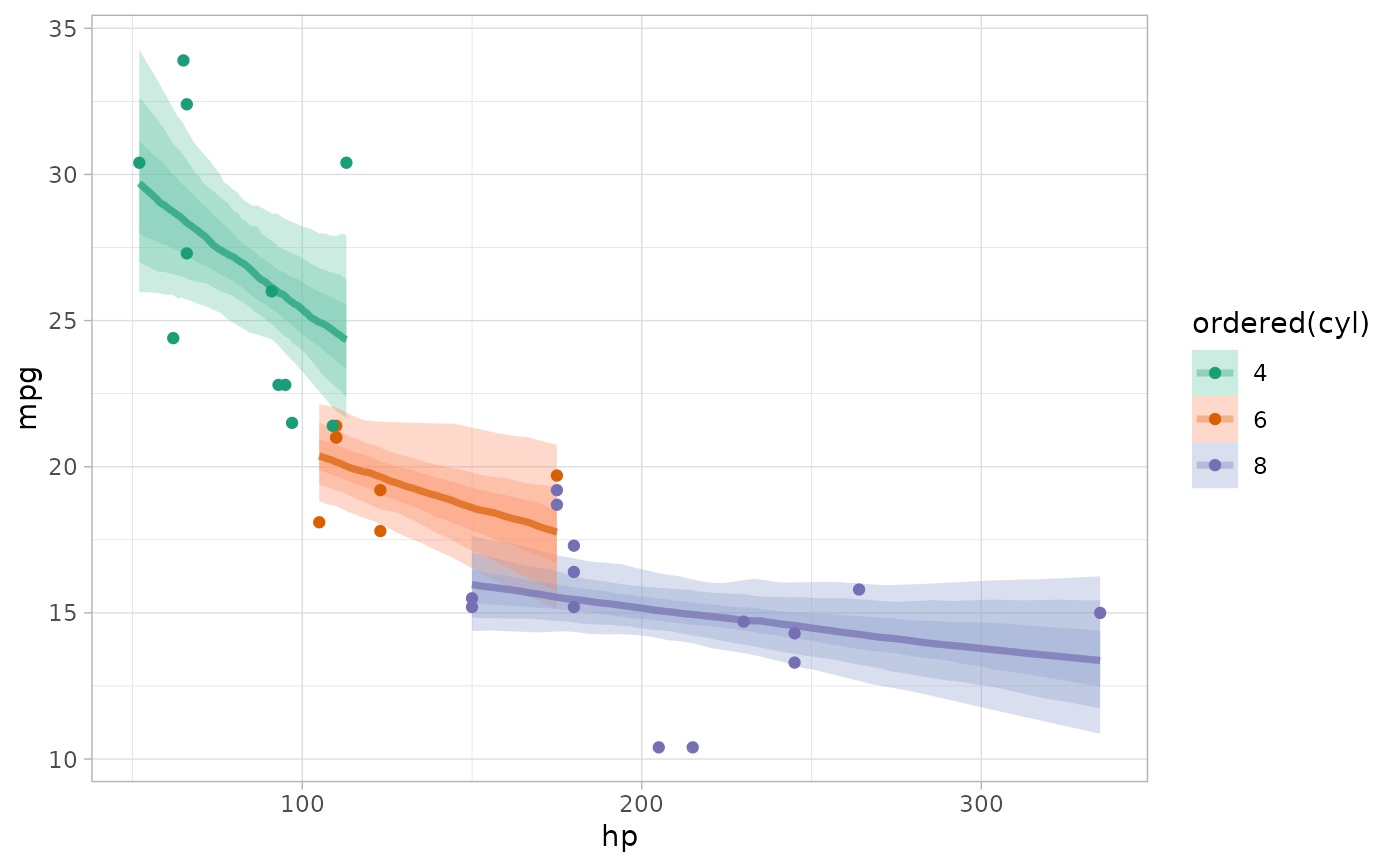
# plot intervals around conditional means (epred_rvars)
mtcars %>%
group_by(cyl) %>%
data_grid(hp = seq_range(hp, n = 101)) %>%
add_epred_rvars(m_mpg) %>%
ggplot(aes(x = hp, color = ordered(cyl), fill = ordered(cyl))) +
stat_lineribbon(aes(dist = .epred), .width = c(.95, .8, .5), alpha = 1/3) +
geom_point(aes(y = mpg), data = mtcars) +
scale_color_brewer(palette = "Dark2") +
scale_fill_brewer(palette = "Set2")
 # plot posterior predictive intervals (predicted_rvars)
mtcars %>%
group_by(cyl) %>%
data_grid(hp = seq_range(hp, n = 101)) %>%
add_predicted_rvars(m_mpg) %>%
ggplot(aes(x = hp, color = ordered(cyl), fill = ordered(cyl))) +
stat_lineribbon(aes(dist = .prediction), .width = c(.95, .8, .5), alpha = 1/3) +
geom_point(aes(y = mpg), data = mtcars) +
scale_color_brewer(palette = "Dark2") +
scale_fill_brewer(palette = "Set2")
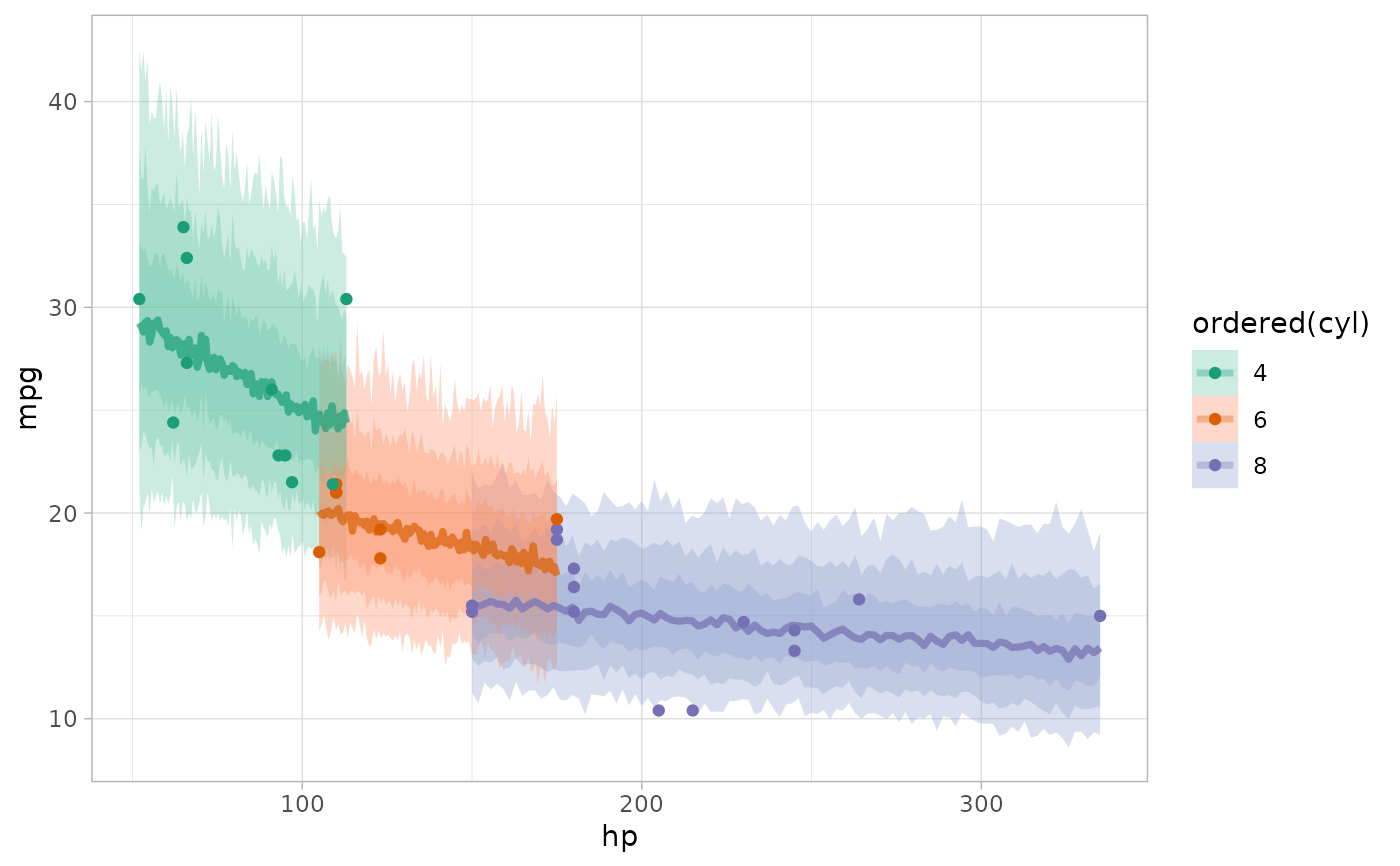
# plot posterior predictive intervals (predicted_rvars)
mtcars %>%
group_by(cyl) %>%
data_grid(hp = seq_range(hp, n = 101)) %>%
add_predicted_rvars(m_mpg) %>%
ggplot(aes(x = hp, color = ordered(cyl), fill = ordered(cyl))) +
stat_lineribbon(aes(dist = .prediction), .width = c(.95, .8, .5), alpha = 1/3) +
geom_point(aes(y = mpg), data = mtcars) +
scale_color_brewer(palette = "Dark2") +
scale_fill_brewer(palette = "Set2")
 # }
# }